
【题目】如图,在平面直角坐标系中,A(3,0),B(0,3),过点B画y轴的垂线l,点C在线段AB上,连结OC并延长交直线l于点D,过点C画CE⊥OC交直线l于点E.
(1)求∠OBA的度数,并直接写出直线AB的解析式;
(2)若点C的横坐标为2,求BE的长;
(3)当BE=1时,求点C的坐标.

【答案】(1)直线AB的解析式为:y=﹣x+3;(2)BE=1;(3)C的坐标为(1,2).
【解析】
(1)根据A(3,0),B(0,3)可得OA=OB=3,得出△AOB是等腰直角三角形,∠OBA=45°,进而求出直线AB的解析式;
(2)作CF⊥l于F,CG⊥y轴于G,利用ASA证明Rt△OGC≌Rt△EFC(ASA),得出EF=OG=1,那么BE=1;
(3)设C的坐标为(m,-m+3).分E在点B的右侧与E在点B的左侧两种情况进行讨论即可.
(1)∵A(3,0),B(0,3),∴OA=OB=3.∵∠AOB=90°,
∴∠OBA=45°,∴直线AB的解析式为:y=﹣x+3;
(2)作CF⊥l于F,CG⊥y轴于G,∴∠OGC=∠EFC=90°.∵点C的横坐标为2,点C在y=﹣x+3上,∴C(2,1),CG=BF=2,OG=1.∵BC平分∠OBE,
∴CF=CG=2.∵∠OCE=∠GCF=90°,∴∠OCG=∠ECF,
∴Rt△OGC≌Rt△EFC(ASA),∴EF=OG=1,∴BE=1;
(3)设C的坐标为(m,﹣m+3).
当E在点B的右侧时,由(2)知EF=OG=m﹣1,
∴m﹣1=﹣m+3,
∴m=2,
∴C的坐标为(2,1);
当E在点B的左侧时,同理可得:m+1=﹣m+3,
∴m=1,
∴C的坐标为(1,2).



 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)之间的函数关系.下列说法中正确的个数是( )
(分钟)之间的函数关系.下列说法中正确的个数是( )
(1)修车时间为15分钟;
(2)学校离家的距离为4000米;
(3)到达学校时共用时间为20分钟;
(4)自行车发生故障时离家距离为2000米.

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为(a,0),(2,﹣4),(c,0),且a,c满足方程![]() 为二元一次方程.
为二元一次方程.
(1)求A,C的坐标.
(2)若点D为y轴正半轴上的一个动点.
①如图1,∠AOD+∠ADO+∠DAO=180°,当AD∥BC时,∠ADO与∠ACB的平分线交于点P,求∠P的度数;
②如图2,连接BD,交x轴于点E.若S△ADE≤S△BCE成立.设动点D的坐标为(0,d),求d的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
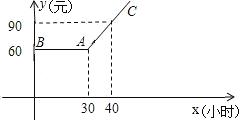
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF。

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,点
,点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两点.将射线
上的两点.将射线![]() 绕点
绕点![]() 顺时针匀速旋转,将射线
顺时针匀速旋转,将射线![]() 绕点
绕点![]() 顺时针匀速旋转,旋转后的射线分别记为
顺时针匀速旋转,旋转后的射线分别记为![]() 、
、![]() ,已知射线
,已知射线![]() 、射线
、射线![]() 旋转的速度之和为6度/秒.
旋转的速度之和为6度/秒.

(1)射线![]() 先转动
先转动![]() 得到射线
得到射线![]() ,然后射线
,然后射线![]() 、
、![]() 再同时旋转10秒,此时射线
再同时旋转10秒,此时射线![]() 与射线
与射线![]() 第一次出现平行.求射线
第一次出现平行.求射线![]() 、
、![]() 的旋转速度;
的旋转速度;
(2)若射线![]() 、
、![]() 分别以(1)中速度同时转动
分别以(1)中速度同时转动![]() 秒,在射线
秒,在射线![]() 与射线
与射线![]() 重合之前,设射线
重合之前,设射线![]() 与射线
与射线![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,
,![]() ,如图2所示.
,如图2所示.
①当![]() 时,求
时,求![]() 、
、![]() 、
、![]() 满足的数量关系;
满足的数量关系;
②当![]() 时,求
时,求![]() 和
和![]() 满足的数量关系.
满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com