
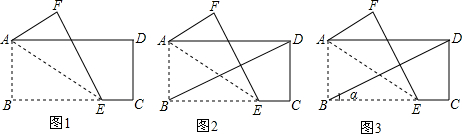
分析 (1)先根据翻折变换的性质得出∠F=90°,∠AEB=∠AEF,故可得出∠BEF的度数,根据平行线的性质得出∠AGF的度数,由直角三角形的性质即可得出结论;
(2)先根据AD∥BC,∠CBD=20°得出∠ADB=20°,再由AF∥BD得出∠FAD=20°,故可得出∠AGF的度数,由平行线的性质得出∠BEF的度数,根据翻折变换的性质得出∠BEA的度数,根据直角三角形的性质即可得出结论;
(3)同(2)的证明过程.
解答  解:(1)如图1,∵△AEF由△AEB反折而成,∠AEB=40°,
解:(1)如图1,∵△AEF由△AEB反折而成,∠AEB=40°,
∴∠F=90°,∠AEB=∠AEF=40°,
∴∠BEF=80°.
∵AD∥BC,
∴∠AGF=∠BEF=80°,
∴∠DAF=90°-80°=10°.
故答案为:10°;
(2)如图2,∵AD∥BC,∠CBD=20°,
∴∠ADB=20°.
∵AF∥BD,
∴∠FAD=20°,
∴∠AGF=90°-20°=70°.
∵AD∥BC,
∴∠BEF=∠AGF=70°.
∵△AEF由△AEB反折而成,
∴∠BEA=$\frac{1}{2}$∠BEF=$\frac{1}{2}$×70°=35°,
∴∠BAE=90°-35°=55°;
(3)如图3,∵AD∥BC,∠CBD=α,
∴∠ADB=α.
∵AF∥BD,
∴∠FAD=α,
∴∠AGF=90°-α.
∵AD∥BC,
∴∠BEF=∠AGF=90°-α.
∵△AEF由△AEB反折而成,
∴∠BEA=$\frac{1}{2}$∠BEF=$\frac{1}{2}$×(90°-α)=45°-$\frac{1}{2}$α,
∴∠BAE=90°-(45°-$\frac{1}{2}$α)=45°+$\frac{1}{2}$α.
故答案为:45°+$\frac{1}{2}$α.
点评 本题考查的是平行线的性质与翻折变换,熟知图形翻折不变性的性质是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
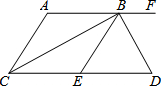 如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论其中错误是( )
如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论其中错误是( )| A. | BC平分∠ABE | B. | AC∥BE | C. | ∠BCD+∠D=90° | D. | ∠DBF=2∠ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.
如图,AB是半圆O的直径,AC⊥AB,CD切半圆于点D,BF⊥AB,交AD的延长线于F,交CD的延长线于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
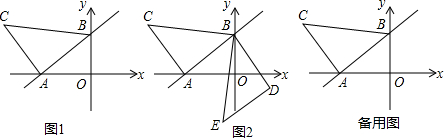
 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com