
【题目】正方形ABCD与正五边形EFGHM的边长相等,初始如图所示,将正方形绕点F顺时针旋转使得BC与FG重合,再将正方形绕点G顺时针旋转使得CD与GH重合…按这样的方式将正方形依次绕点H、M、E旋转后,正方形中与EF重合的是( )
A.AB
B.BC
C.CD
D.DA
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() ﹣(+2
﹣(+2![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(﹣0.75);
)﹣(﹣0.75);
(2)(![]() ﹣
﹣![]() +
+![]() )×(﹣78);
)×(﹣78);
(3)(﹣![]() )÷(1
)÷(1![]() ﹣
﹣![]() ﹣
﹣![]() );
);
(4)﹣32﹣2÷![]() ×[2﹣(﹣
×[2﹣(﹣![]() )2]﹣(﹣2)3.
)2]﹣(﹣2)3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成五个扇形,五个扇形内部分别标有数字.﹣2、3、﹣4、5.若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为m,n(当指针指在边界线时视为无效,重转),从而确定一个点的坐标为A(m,n).请用列表或者画树状图的方法求出所有可能得到的点A的坐标,并求出点A在第一象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元,若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸每个小方格是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(a,b)D(1,4).
(1)描出A、B、C、D四点的位置.如图,则a= ;b= ;
(2)四边形ABCD的面积是 ;(直接写出结果)
(3)把四边形ABCD向左平移6个单位,再向下平移1个单位得到四边形A'B'C'D',在图中画出四边形A'B'C'D',并写出A'B'C'D'的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线AC﹣BC是一条公路的示意图,AC=8km,甲骑摩托车从A地沿这条公路到B地,速度为40km/h,乙骑自行车从C地到B地,速度为10km/h,两人同时出发,结果甲比乙早到6分钟.
(1)求这条公路的长;
(2)设甲乙出发的时间为t小时,求甲没有超过乙时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻教育部关于中小学生“每天锻炼一小时”的要求,某市教育局做了一次随机抽样调查,其内容是:(1)学生每天锻炼时间是否达到1小时;(2)学生每天锻炼时间未达到1小时的原因.随机调查了600名学生,把所得的数据制成了如下的扇形统计图和条形统计图(不完整)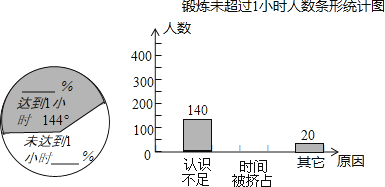
根据图示,回答以下问题:
(1)每天锻炼时间达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数占被调查总人数的百分比是;
每天锻炼时间未达到1小时的人数为人,其中原因是“时间被挤占”的人数是人;
(2)补全扇形统计图和条形统计图;
(3)若该市现有中小学生约27万人,据此调查,可估计今年该市中小学生每天锻炼未达到1小时的学生约有多少万人?
(4)从这次接受调查的学生中,随机抽取一名学生的“每天锻炼一小时”的情况,回答内容为“时间被挤占”的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com