
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ĖıߊĪABCDĖÄĢõ±ßÉĻµÄÖŠµć·Ö±šĪŖE”¢F”¢G”¢H£¬Ė³“ĪĮ¬½ÓEF”¢FG”¢GH”¢HE£¬µĆµ½ĖıߊĪEFGH£Ø¼“ĖıߊĪABCDµÄÖŠµćĖıߊĪ£©£®
£Ø1£©ĖıߊĪEFGHµÄŠĪדŹĒ_____£¬
Ö¤Ć÷ÄćµÄ½įĀŪ£®
£Ø2£©µ±ĖıߊĪABCDµÄ¶Ō½ĒĻßĀś×ć_____Ģõ¼žŹ±£¬ĖıߊĪEFGHŹĒ¾ŲŠĪ£»
£Ø3£©µ±ĖıߊĪABCDµÄ¶Ō½ĒĻßĀś×ć_____Ģõ¼žŹ±£¬ĖıߊĪEFGHŹĒĮāŠĪ£»
£Ø4£©Äćѧ¹żµÄÄÄÖÖĢŲŹāĖıߊĪµÄÖŠµćĖıߊĪŹĒ¾ŲŠĪ£æ_____£»
£Ø5£©Äćѧ¹żµÄÄÄÖÖĢŲŹāĖıߊĪµÄÖŠµćĖıߊĪŹĒĮāŠĪ£æ_____£»
£Ø6£©Äćѧ¹żµÄÄÄÖÖĢŲŹāĖıߊĪµÄÖŠµćĖıߊĪŹĒÕż·½ŠĪ£æ_____£®

”¾“š°ø”æ Ę½ŠŠĖıߊĪ AC”ĶBD AC=BD ĮāŠĪ ¾ŲŠĪ Õż·½ŠĪ
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©Į¬½ÓBD£¬øł¾ŻČż½ĒŠĪµÄÖŠĪ»Ļß¶ØĄķµĆµ½EH”ĪBD£¬EH=![]() BD£¬FG”ĪBD£¬FGØT
BD£¬FG”ĪBD£¬FGØT![]() BD£¬ĶĘ³ö£¬EH”ĪFG£¬EH=FG£¬øł¾ŻŅ»×é¶Ō±ßĘ½ŠŠĒŅĻąµČµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪµĆ³öĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
BD£¬ĶĘ³ö£¬EH”ĪFG£¬EH=FG£¬øł¾ŻŅ»×é¶Ō±ßĘ½ŠŠĒŅĻąµČµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪµĆ³öĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©øł¾ŻÓŠŅ»øö½ĒŹĒÖ±½ĒµÄĘ½ŠŠĖıߊĪŹĒ¾ŲŠĪ£¬æÉÖŖµ±ĖıߊĪABCDµÄ¶Ō½ĒĻßĀś×ćAC”ĶBDµÄĢõ¼žŹ±£¬ĖıߊĪEFGHŹĒ¾ŲŠĪ£»
£Ø3£©Ģķ¼ÓµÄĢõ¼žÓ¦ĪŖ£ŗAC=BD£¬°ŃAC=BD×÷ĪŖŅŃÖŖĢõ¼ž£¬øł¾ŻČż½ĒŠĪµÄÖŠĪ»Ļß¶ØĄķæÉµĆ£¬HGĘ½ŠŠĒŅµČÓŚACµÄŅ»°ė£¬EFĘ½ŠŠĒŅµČÓŚACµÄŅ»°ė£¬øł¾ŻµČĮæ“ś»»ŗĶĘ½ŠŠÓŚĶ¬Ņ»ĢõÖ±ĻßµÄĮ½Ö±ĻßĘ½ŠŠ£¬µĆµ½HGŗĶEFĘ½ŠŠĒŅĻąµČ£¬ĖłŅŌEFGHĪŖĘ½ŠŠĖıߊĪ£¬ÓÖEHµČÓŚBDµÄŅ»°ėĒŅAC=BD£¬ĖłŅŌµĆµ½ĖłÖ¤ĖıߊĪµÄĮŚ±ßEHÓėHGĻąµČ£¬ĖłŅŌĖıߊĪEFGHĪŖĮāŠĪ£®
£Ø4£©ĮāŠĪµÄÖŠµćĖıߊĪŹĒ¾ŲŠĪ£®øł¾ŻČż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚµŚČż±ß²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ėæɵĆEH”ĪBD£¬EF”ĪAC£¬ŌŁøł¾Ż¾ŲŠĪµÄĆæŅ»øö½Ē¶¼ŹĒÖ±½ĒæɵƔĻ1=90”ć£¬Č»ŗóøł¾ŻĘ½ŠŠĻߵĊŌÖŹĒó³ö”Ļ3=90”ć£¬ŌŁøł¾Ż“¹Ö±¶ØŅå½ā“š£»
£Ø5£©ĮāŠĪµÄÖŠµćĖıߊĪŹĒ¾ŲŠĪ£®øł¾ŻČż½ĒŠĪµÄÖŠĪ»ĻßĘ½ŠŠÓŚµŚČż±ß²¢ĒŅµČÓŚµŚČż±ßµÄŅ»°ėæɵĆEH”ĪBD£¬EF”ĪAC£¬ŌŁøł¾Ż¾ŲŠĪµÄĆæŅ»øö½Ē¶¼ŹĒÖ±½ĒæɵƔĻ1=90”ć£¬Č»ŗóøł¾ŻĘ½ŠŠĻߵĊŌÖŹĒó³ö”Ļ3=90”ć£¬ŌŁøł¾Ż“¹Ö±¶ØŅå½ā“š£»
£Ø6£©øł¾ŻĮŚ±ßĻąµČµÄ¾ŲŠĪĪŖÕż·½ŠĪ½ųŠŠ½ā“š£®
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©ĖıߊĪEFGHµÄŠĪדŹĒĘ½ŠŠĖıߊĪ£®ĄķÓÉČēĻĀ£ŗ
ČēĶ¼£¬Į¬½įBD£®”ßE”¢H·Ö±šŹĒAB”¢ADÖŠµć£¬”ąEH”ĪBD£¬EH=![]() BD£¬Ķ¬ĄķFG”ĪBD£¬FG=
BD£¬Ķ¬ĄķFG”ĪBD£¬FG=![]() BD£¬”ąEH”ĪFG£¬EH=FG£¬”ąĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
BD£¬”ąEH”ĪFG£¬EH=FG£¬”ąĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©µ±ĖıߊĪABCDµÄ¶Ō½ĒĻßĀś×滄Ļą“¹Ö±µÄĢõ¼žŹ±£¬ĖıߊĪEFGHŹĒ¾ŲŠĪ£®ĄķÓÉČēĻĀ£ŗ
ČēĶ¼£¬Į¬½įAC”¢BD£®”ßE”¢F”¢G”¢H·Ö±šĪŖĖıߊĪABCDĖÄĢõ±ßÉĻµÄÖŠµć£¬”ąEH”ĪBD£¬HG”ĪAC£®”ßAC”ĶBD£¬”ąEH”ĶHG£®ÓÖ”ßĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£¬”ąĘ½ŠŠĖıߊĪEFGHŹĒ¾ŲŠĪ£»
£Ø3£©”ßE£¬F£¬G£¬H·Ö±šŹĒ±ßAB”¢BC”¢CD”¢DAµÄÖŠµć£¬”ąŌŚ”÷ADCÖŠ£¬HGĪŖ”÷ADCµÄÖŠĪ»Ļߣ¬ĖłŅŌHG”ĪACĒŅHG=![]() AC£»Ķ¬ĄķEF”ĪACĒŅEF=
AC£»Ķ¬ĄķEF”ĪACĒŅEF=![]() AC£¬Ķ¬ĄķæɵĆEH=
AC£¬Ķ¬ĄķæɵĆEH=![]() BD£¬ŌņHG”ĪEFĒŅHG=EF£¬”ąĖıߊĪEFGHĪŖĘ½ŠŠĖıߊĪ£¬ÓÖAC=BD£¬ĖłŅŌEF=EH£¬”ąĖıߊĪEFGHĪŖĮāŠĪ£®
BD£¬ŌņHG”ĪEFĒŅHG=EF£¬”ąĖıߊĪEFGHĪŖĘ½ŠŠĖıߊĪ£¬ÓÖAC=BD£¬ĖłŅŌEF=EH£¬”ąĖıߊĪEFGHĪŖĮāŠĪ£®
£Ø4£©ĮāŠĪµÄÖŠµćĖıߊĪŹĒ¾ŲŠĪ£®ĄķÓÉČēĻĀ£ŗ
ČēĶ¼£¬Į¬½įAC”¢BD£®”ßE”¢F”¢G”¢H·Ö±šĪŖĖıߊĪABCDĖÄĢõ±ßÉĻµÄÖŠµć£¬span>”ąEH”ĪBD£¬HG”ĪAC£¬FG”ĪBD£¬EH=![]() BD£¬FG=
BD£¬FG=![]() BD£¬”ąEH”ĪFG£¬EH=FG£¬”ąĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£®
BD£¬”ąEH”ĪFG£¬EH=FG£¬”ąĖıߊĪEFGHŹĒĘ½ŠŠĖıߊĪ£®
”ßĖıߊĪABCDŹĒĮāŠĪ£¬”ąAC”ĶBD£®”ßEH”ĪBD£¬HG”ĪAC£¬”ąEH”ĶHG£¬”ąĘ½ŠŠĖıߊĪEFGHŹĒ¾ŲŠĪ£»
£Ø5£©¾ŲŠĪµÄÖŠµćĖıߊĪŹĒĮāŠĪ£®ĄķÓÉČēĻĀ£ŗ
ĄķÓÉČēĻĀ£ŗ
ČēĶ¼£¬Į¬½ÓAC”¢BD£®ŌŚ”÷ABDÖŠ£¬”ßAH=HD£¬AE=EB£¬”ąEH=![]() BD£¬Ķ¬ĄķFG=
BD£¬Ķ¬ĄķFG=![]() BD£¬HG=
BD£¬HG=![]() AC£¬EF=
AC£¬EF=![]() AC£®ÓÖ”ßŌŚ¾ŲŠĪABCDÖŠ£¬AC=BD£¬”ąEH=HG=GF=FE£¬”ąĖıߊĪEFGHĪŖĮāŠĪ£®
AC£®ÓÖ”ßŌŚ¾ŲŠĪABCDÖŠ£¬AC=BD£¬”ąEH=HG=GF=FE£¬”ąĖıߊĪEFGHĪŖĮāŠĪ£®
£Ø6£©Į¬½ÓAC”¢BD£®”ßE”¢F”¢G”¢H·Ö±šŹĒAB”¢BC”¢CD”¢DAµÄÖŠµć£¬”ąEF=![]() AC£¬GH=
AC£¬GH=![]() AC£¬EH=
AC£¬EH=![]() BD£¬GF=
BD£¬GF=![]() BD£®”ßAB=CD£¬”ąAC=BD£¬”ąEF=GH=EH=GF£¬”ąĖıߊĪEFGHĮāŠĪ£®”ß”ĻHEF=90”ć£¬”ąĖıߊĪEFGHÕż·½ŠĪ£®¹Ź“š°øĪŖ£ŗĘ½ŠŠĖıߊĪ£»AC”ĶBD£»AC=BD£»ĮāŠĪ£»¾ŲŠĪ£»Õż·½ŠĪ£®
BD£®”ßAB=CD£¬”ąAC=BD£¬”ąEF=GH=EH=GF£¬”ąĖıߊĪEFGHĮāŠĪ£®”ß”ĻHEF=90”ć£¬”ąĖıߊĪEFGHÕż·½ŠĪ£®¹Ź“š°øĪŖ£ŗĘ½ŠŠĖıߊĪ£»AC”ĶBD£»AC=BD£»ĮāŠĪ£»¾ŲŠĪ£»Õż·½ŠĪ£®



 Š”ѧ½Ģ²ÄČ«²āĻµĮŠ“š°ø
Š”ѧ½Ģ²ÄČ«²āĻµĮŠ“š°ø Š”ѧŹżŃ§æŚĖćĢāæØĶŃæŚ¶ų³öĻµĮŠ“š°ø
Š”ѧŹżŃ§æŚĖćĢāæØĶŃæŚ¶ų³öĻµĮŠ“š°ø ÓÅŠćÉśÓ¦ÓĆĢāæØæŚĖćĢģĢģĮ·ĻµĮŠ“š°ø
ÓÅŠćÉśÓ¦ÓĆĢāæØæŚĖćĢģĢģĮ·ĻµĮŠ“š°ø Õć½Ö®ŠĒæĪŹ±ÓÅ»Æ×÷ŅµĻµĮŠ“š°ø
Õć½Ö®ŠĒæĪŹ±ÓÅ»Æ×÷ŅµĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬Ö±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() .
.
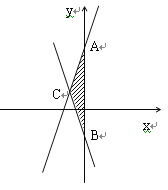
”¾1”æ£Ø1£©ĒóĮ½Ö±ĻßÓė![]() Öį½»µćA£¬BµÄ×ų±ź;
Öį½»µćA£¬BµÄ×ų±ź;
”¾2”æ£Ø2£©ĒóĮ½Ö±Ļß½»µćCµÄ×ų±ź;
”¾3”æ£Ø3£©Ēó”÷ABCµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĮāŠĪ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ”¢
”¢![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ĒŅ
ĒŅ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() .
.
(1)ĒóÖ¤:![]() ;
;
(2)ČōĮāŠĪ![]() µÄ±ß³¤ĪŖ2,
µÄ±ß³¤ĪŖ2, ![]() .Ēó
.Ēó![]() µÄ³¤.
µÄ³¤.

”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£Ø2£©![]()
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ĻČĒó³öĖıߊĪOCEDŹĒĘ½ŠŠĖıߊĪ£¬ŌŁøł¾ŻĮāŠĪµÄ¶Ō½ĒĻß»„Ļą“¹Ö±Ēó³ö”ĻCOD=90”ć£¬Ö¤Ć÷OCEDŹĒ¾ŲŠĪ£¬æɵĆOE=CD¼“æÉ£»
£Ø2£©øł¾ŻĮāŠĪµÄŠŌÖŹµĆ³öAC=AB£¬ŌŁøł¾Ż¹“¹É¶ØĄķµĆ³öAEµÄ³¤¶Č¼“æÉ£®
£Ø1£©Ö¤Ć÷£ŗŌŚĮāŠĪABCDÖŠ£¬OC=![]() AC£®
AC£®
”ąDE=OC£®
”ßDE”ĪAC£¬
”ąĖıߊĪOCEDŹĒĘ½ŠŠĖıߊĪ£®
”ßAC”ĶBD£¬
”ąĘ½ŠŠĖıߊĪOCEDŹĒ¾ŲŠĪ£®
”ąOE=CD£®
£Ø2£©ŌŚĮāŠĪABCDÖŠ£¬”ĻABC=60”ć£¬
”ąAC=AB=2£®
”ąŌŚ¾ŲŠĪOCEDÖŠ£¬
CE=OD=![]() £®
£®
ŌŚRt”÷ACEÖŠ£¬
AE=![]() £®
£®
µć¾¦£ŗ±¾Ģāæ¼²éĮĖĮāŠĪµÄŠŌÖŹ£¬¾ŲŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬¹“¹É¶ØĄķµÄÓ¦ÓĆ£¬ŹĒ»ł“”Ģā£¬Źģ¼Ē¾ŲŠĪµÄÅŠ¶Ø·½·ØÓėĮāŠĪµÄŠŌÖŹŹĒ½āĢāµÄ¹Ų¼ü£®
”¾ĢāŠĶ”æ½ā“šĢā
”¾½įŹų”æ
25
”¾ĢāÄæ”æČēĶ¼£¬·“±ČĄżŗÆŹży=![]() µÄĶ¼ĻóÓėŅ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó½»ÓŚA£¬BĮ½µć£¬µćAµÄ×ų±źĪŖ£Ø2£¬6£©£¬µćBµÄ×ų±źĪŖ£Øn£¬1£©£®
µÄĶ¼ĻóÓėŅ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó½»ÓŚA£¬BĮ½µć£¬µćAµÄ×ų±źĪŖ£Ø2£¬6£©£¬µćBµÄ×ų±źĪŖ£Øn£¬1£©£®
£Ø1£©Ē󷓱ȥżŗÆŹżÓėŅ»“ĪŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©½įŗĻĶ¼ĻńŠ“³ö²»µČŹ½![]() µÄ½ā¼Æ£»
µÄ½ā¼Æ£»
£Ø3£©µćEĪŖyÖįÉĻŅ»øö¶Æµć£¬ČōS”÷AEB=10£¬ĒóµćEµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹¤³§¼Ę»®Éś²śA£¬BĮ½ÖÖ²śĘ·¹²10¼ž£¬ĘäÉś²ś³É±¾ŗĶĄūČóČēĻĀ±ķ£ŗ
AÖÖ²śĘ· | BÖÖ²śĘ· | |
³É±¾£ØĶņŌŖ/¼ž£© | 2 | 5 |
ĄūČó£ØĶņŌŖ/¼ž£© | 1 | 3 |
£Ø1£©Čō¹¤³§¼Ę»®»ńĄū14ĶņŌŖ£¬ĪŹA£¬BĮ½ÖÖ²śĘ·Ó¦·Ö±šÉś²ś¶ąÉŁ¼ž£æ
£Ø2£©Čō¹¤³§¼Ę»®Ķ¶Čė׏½š²»¶ąÓŚ44ĶņŌŖ£¬ĒŅ»ńĄū¶ąÓŚ14ĶņŌŖ£¬ĪŹ¹¤³§ÓŠÄļøÖÖÉś²ś·½°ø£æ
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ÄÄÖÖÉś²ś·½°ø»ńĄū×ī“ó£æ²¢Ēó³ö×ī“óĄūČó£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬·½øńÖ½ÖŠĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄÕż·½ŠĪ£¬”÷ABCµÄ¶„µćŗĶµćO¾łŌŚĶųøńĶ¼µÄøńµćÉĻ£¬½«”÷ABCČʵćOÄꏱÕėŠż×Ŗ90”ć£¬µĆµ½”÷A1B1C1 £® 
£Ø1£©Ēė»³ö”÷A1B1C1£»
£Ø2£©ŅŌµćOĪŖŌ²ŠÄ£¬ ![]() ĪŖ°ė¾¶×÷”ŃO£¬ĒėÅŠ¶ĻÖ±ĻßAA1Óė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
ĪŖ°ė¾¶×÷”ŃO£¬ĒėÅŠ¶ĻÖ±ĻßAA1Óė”ŃOµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬AB=10£¬”ĻABC=60”ć£®µćP“ÓµćBŃŲBCŅŌĆæĆė1øöµ„Ī»³¤µÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬ÉäĻßPFĖęµćPŅĘ¶Æ£¬Ź¼ÖÕ±£³ÖÓėBC“¹Ö±£¬²¢½»ÕŪĻßBA©ACÓŚµćE£¬½»Ö±ĻßADÓŚµćF£®ÉčµćPŌĖ¶ÆŹ±¼äĪŖtĆė£¬ĒŅµćPÖ»ŌŚBCÉĻŌĖ¶Æ£®
£Ø1£©µ±tĪŖŗĪÖµŹ±£¬BP=AF£æ
£Ø2£©ÉčÖ±ĻßPFÉعżĮāŠĪABCDµÄĆ껿ĪŖS£¬ŹŌÓĆtµÄŹ½×Ó±ķŹ¾S£®£ØŠ“½āĢā¹ż³Ģ£©



²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¶ÖĄŅ»Ć¶ÖŹµŲ¾łŌȵÄÕż·½Ģå÷»×Ó£®
£Ø1£©ĻĀĮŠĖµ·ØÖŠÕżČ·µÄÓŠ £® £ØĢīŠņŗÅ£©
¢ŁĻņÉĻŅ»ĆęµćŹżĪŖ1µćŗĶ3µćµÄæÉÄÜŠŌŅ»Ńł“ó£»
¢ŚĶ¶ÖĄ6“Ī£¬ĻņÉĻŅ»ĆęµćŹżĪŖ1µćµÄŅ»¶Ø»į³öĻÖ1“Ī£»
¢ŪĮ¬ŠųĶ¶ÖĄ2“Ī£¬ĻņÉĻŅ»ĆęµÄµćŹżÖ®ŗĶ²»æÉÄܵČÓŚ13£®
£Ø2£©Čē¹ūŠ”Ć÷Į¬ŠųĶ¶ÖĄĮĖ10“Ī£¬ĘäÖŠÓŠ3“Ī³öĻÖĻņÉĻŅ»ĆęµćŹżĪŖ6µć£¬ÕāŹ±Š”Ć÷Ėµ£ŗĶ¶ÖĄÕż·½Ģå÷»×Ó£¬ĻņÉĻŅ»ĆęµćŹżĪŖ6µćµÄøÅĀŹŹĒ![]() £® ÄćĶ¬ŅāĖūµÄĖµ·ØĀš£æĖµĖµÄćµÄĄķÓÉ£®
£® ÄćĶ¬ŅāĖūµÄĖµ·ØĀš£æĖµĖµÄćµÄĄķÓÉ£®
£Ø3£©ĪŖĮĖ¹Ą¼ĘĶ¶ÖĄÕż·½Ģå÷»×Ó³öĻÖ6µć³ÆÉĻµÄøÅĀŹ£¬Š”ĮĮ²ÉÓĆ×ŖÅĢĄ““śĢę÷»×Ó×öŹµŃ飮ĻĀĶ¼ŹĒŅ»øöæÉŅŌ×ŌÓÉ×Ŗ¶ÆµÄ×ŖÅĢ£¬ĒėÄć½«×ŖÅĢ·ÖĪŖ2øöÉČŠĪĒųÓņ£¬·Ö±šĶæÉĻŗģ”¢°×Į½ÖÖŃÕÉ«£¬Ź¹µĆ×Ŗ¶Æ×ŖÅĢ£¬µ±×ŖÅĢĶ£Ö¹×Ŗ¶Æŗó£¬ÖøÕėĀäŌŚŗģÉ«ĒųÓņµÄøÅĀŹÓėĶ¶ÖĄÕż·½Ģå÷»×Ó³öĻÖ6µć³ÆÉĻµÄøÅĀŹĻąĶ¬£®£ØÓŃĒéĢįŠŃ£ŗŌŚ×ŖÅĢÉĻÓĆĪÄ×Ö×¢Ć÷ŃÕÉ«ŗĶÉČŠĪŌ²ŠÄ½ĒµÄ¶ČŹż£®£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
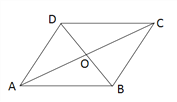
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AD=12£¬DO=OB=£µ£¬AC=26£¬”ĻADB=90”ć.ĒóBCµÄ³¤ŗĶĖıߊĪABCDµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«Į½Ģõæķ¶Č¶¼ĪŖ3µÄÖ½ĢõÖŲµžŌŚŅ»Ęš£¬Ź¹”ĻABC=60”ć£¬ŌņĖıߊĪABCDµÄĆ껿ĪŖ £®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com