
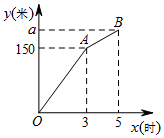
 甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队独自完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.
甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队独自完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)(2)根据图象解答即可;
(3)根据题意得出甲、乙两队每小时维修路面的总长度解答即可;
(4)设所求函数关系式y=kx+b,利用待定系数法解答即可.
解答 解:(1)由图象知,甲队调离时,甲、乙两队已维修路面的总长度为150米,故(1)正确;
(2)由图象知,甲乙共同工作3小时,乙又工作2小时,乙工作5小时,故(2)错误;
(3)∵甲乙共同工作3小时共维修150米,甲维修3×30米=90米,乙甲队每小时维修路面(150-90)÷3米=20米,2小时维修2×20米=40米,
∴a=150米+20米=190米,故(3)正确;
(4)∵A(3,150),B(5,190),设AB的函数关系式为y=kx+b,
将点(3,150),(5,190)代入,得$\left\{\begin{array}{l}{3k+b=150}\\{5k+b=190}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=20}\\{b=90}\end{array}\right.$,
∴y=20x+90(3<x≤5),
故(4)正确;
故选C.
点评 本题考查了一次函数的应用,解决本题的关键是读懂图象,获取相关信息,用待定系数法求函数解析式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于点A,B,交y轴于点C,四边形OCDB为正方形,点D的坐标为(6,6).
已知抛物线y=-$\frac{1}{2}$x2+bx+c交x轴于点A,B,交y轴于点C,四边形OCDB为正方形,点D的坐标为(6,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=54x(x>2) | B. | y=54x+10(x>2) | C. | y=54x-90(x>2) | D. | y=54x+45(x>2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com