
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
【答案】(1)y=﹣x+180;(2)y=(x﹣100)(﹣x+180)售价定为140元/件时,每天最大利润W=1600元.
【解析】(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于kb的关系式,求出k、b的值即可;
(2)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由所给函数图象可知,
![]() ,解得
,解得![]() .
.
故y与x的函数关系式为y=﹣x+180;
(2)∵y=﹣x+180,
∴W=(x﹣100)y=(x﹣100)(﹣x+180)
=﹣x2+280x﹣18000
=﹣(x﹣140)2+1600,
∵a=﹣1<0,
∴当x=140时,W最大=1600,
∴售价定为140元/件时,每天最大利润W=1600元.


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交直线BD于点F.

(1)如图1,若四边形ABCD是正方形,判断AF与BE的数量关系:AF与BE的数量关系是 ;
(2)如图2,若四边形ABCD是菱形,∠ABC=120°,求![]() 的值;
的值;
(3)如图3,若四边形ABCD中,AC⊥BD,∠ABC=α,∠DBC=β,请你补全图形,并直接写出:![]() = (用含α,β的式子表示).
= (用含α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列填空.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 (已知)
∴ (等量代换)
∴DG∥BA. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
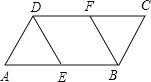
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com