解:(1)①△ABD与△DEC相似,
理由:∵在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵∠ADC=∠B+∠BAD=∠ADE+∠EDC,∠ADF=45°,
∴∠BAD=∠EDC,
∴△ABD∽△DEC;
②作AH⊥BC,垂足为H,如图1,
易知△ABH是等腰直角三角形,
∵AB=

,
∴AH=2,△ABD的面积为

,
∵DC=4-x,△ABD∽△DCE,
∴

,
∴
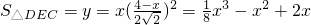
;
(2)(Ⅰ)D在线段BC上,
①AD=AE,此时B、D重合,不合题意,
②若AD=DE,如图2,
∵由(1)①得△ABD∽△DCE,
∴△ABD≌△DCE,
∴DC=AB=

,
∴BD=4-

,
③若AE=DE,如图3,
∵∠ADF=45°,
∴易得△ADE是等腰直角三角形,
∴△ABD也是等腰直角三角形,

∴BD=2;
(Ⅱ)D在线段BC的延长线上,
∵∠ADF=45°,
∴∠ADE=135°,
∴只有AD=DE,如图4,
∵由(1)①得△ABD∽△DCE,
∴△ABD≌△DCE,
∴DC=AB=

,
∴BD=4+

,
综上:BD=2,4-

,4+

.
分析:(1)相似;根据三角形外角的性质即可得到∠ADC=∠B+∠BAD=∠ADE+∠EDC,从而得到∠BAD=∠EDC,进而得到两三角形相似.
(2)分D在线段BC上和D在线段BC的延长线上,两种情况讨论即可得到BD为何值时,△ADE是等腰三角形.
点评:本题考查了相似三角形的判定及性质、全等三角形的判定及性质、等腰直角三角形的性质等知识,是一道综合性较强的题目,难度较大.

 在Rt△ABC中,∠BAC=90°,AB=AC=
在Rt△ABC中,∠BAC=90°,AB=AC= ,D是射线BC上一点,在DA的顺时针方向作∠ADF=45°,DF所在的直线与射线AC交于点E.
,D是射线BC上一点,在DA的顺时针方向作∠ADF=45°,DF所在的直线与射线AC交于点E. ,
, ,
, ,
,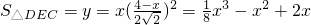 ;
; ,
, ,
,
 ,
, ,
, ,4+
,4+ .
.

 名校课堂系列答案
名校课堂系列答案