
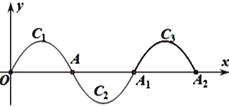
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
【答案】-1
【解析】
每次变化时,开口方向变化但形状不变,则 ![]() ,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式
,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式![]() 求得解析式,把x=4035代入解析式,即可求得m的值.
求得解析式,把x=4035代入解析式,即可求得m的值.
由抛物线C1:y=-x(x-2),
令y=0,∴-x(x-2)=0,解得 ![]()
∴与x轴的交点为O(0,0),A(2,0).
抛物线C2的开口向上,且与x轴的交点为∴A(2,0)和A1(4,0),
则抛物线C2:y= (x-2)(x-4);
抛物线C3的开口向下,且与x轴的交点为∴A1(4,0)和A2(6,0),
则抛物线C3:y= -(x-4)(x-6);
抛物线C4的开口向上,且与x轴的交点为∴A2(6,0)和A3(8,0),
则抛物线C4:y=(x-6)(x-8);
同理:
抛物线C2018的开口向上,且与x轴的交点为∴A2016(4034,0)和A2017(4036,0),
则抛物线C2018:y=(x-4034)(x-4036);
当x=4035时,y= 1×(-1)-1.
故答案为:-1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
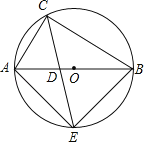
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市去年成功举办2018郴州国际休闲旅游文化节,获评“全国森林旅游示范市”.某市有A,B,C,D,E五个景区很受游客喜爱.一旅行社对某小区居民在暑假期间去以上五个景区旅游(只选一个景区)的意向做了一次随机调查统计,并根据这个统计结果制作了如下两幅不完整的统计图:
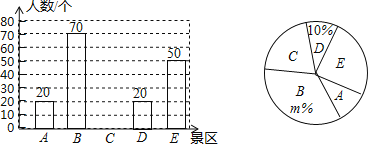
(1)该小区居民在这次随机调查中被调查到的人数是 人,![]() ,并补全条形统计图;
,并补全条形统计图;
(2)若该小区有居民1200人,试估计去B地旅游的居民约有多少人?
(3)小军同学已去过E地旅游,暑假期间计划与父母从A,B,C,D四个景区中,任选两个去旅游,求选到A,C两个景区的概率.(要求画树状图或列表求概率)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)在直线l上确定一点P,使△PAC的周长最小,求出点P的坐标.
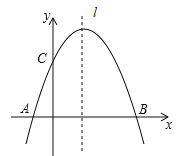
查看答案和解析>>
科目:初中数学 来源: 题型:
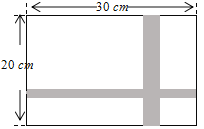
【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
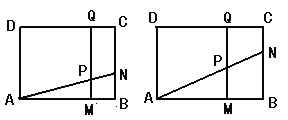
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
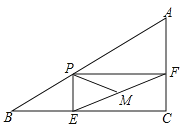
【题目】在Rt△ABC中,∠C=90°,AB=5,AC=3,点P为边AB上一动点(且点P不与点A,B重合),PE⊥BC于E,PF⊥AC于F,点M为EF中点,则PM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com