
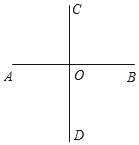
【题目】操作:如图,直线AB与CD交于点O,按要求完成下列问题.
(1)用量角器量得∠AOC= 度.AB与CD的关系可记作 .
(2)画出∠BOC的角平分线OM,∠BOM=∠ = 度.
(3)在射线OM上取一点P,画出点P到直线AB的距离PE.
(4)如图若按“上北下南左西右东”的方位标记,请画出表示“南偏西30°”的射线OF.
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数 | 6 | 10 | 12 | |
棱数 | 9 | 12 | ||
面数 | 5 | 8 |
观察上表中的结果,你能发现![]() 、
、![]() 、
、之间有什么关系吗?请写出关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:菱形的两条对角线互相垂直. 已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.
求证:AC⊥BD.
以下是排乱的证明过程:
①又BO=DO;
②∴AO⊥BD,即AC⊥BD;
③∵四边形ABCD是菱形;
④∴AB=AD.
证明步骤正确的顺序是( )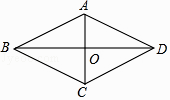
A.③→②→①→④
B.③→④→①→②
C.①→②→④→③
D.①→④→③→②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p. ![]()
(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
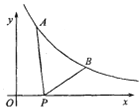
【题目】如图,已知点A(![]() ,y1)、B(2,y2)在反比例函数y=
,y1)、B(2,y2)在反比例函数y=![]() 的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
A. (![]() ,0) B. (
,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若AC+BC=acm,其他条件不变,直接写出线段MN的长为 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中有一个黑球a和两个白球b,c(除颜色外其他均相同).用树状图(或列表法)解答下列问题:
(1)小丽第一次从袋子中摸出一个球不放回,第二次又从袋子中摸出一个球.则小丽两次都摸到白球的概率是多少?
(2)小强第一次从袋子中摸出一个球,摸到黑球不放回,摸到白球放回;第二次又从袋子中摸出一个球,则小强两次都摸到白球的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中有四点A(﹣2,0),B(﹣1,0),C(0,1),D(0,2)在A、B、C、D中取两点与点O为顶点作三角形,所作三角形是等腰直角三角形的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a,b,c分别满足:-(a-4)2≥0,c=![]() +
+![]() +8.
+8.
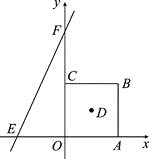
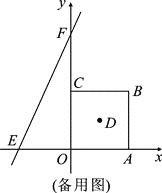
(1)直线y=bx+c的解析式为________;正方形OABC的对角线的交点D的坐标为________;
(2)若正方形OABC沿x轴负方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,在备用图中画图分析,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com