

| 1 |
| 2 |
| 1 |
| 2 |
| OA2+OB2 |
| 62+82 |
| OA2+OD32 |
| 62+22 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 1 |
| 2 |
3
| ||
| 5 |
3
| ||
| 5 |
6
| ||
| 5 |
| OF |
| OA |
| CF |
| OD3 |
| OC |
| AD3 |
| OF |
| 6 |
| CF |
| 2 |
| ||||
2
|
| 3 |
| 5 |
| 18 |
| 5 |
| 6 |
| 5 |
| 18 |
| 5 |
| 6 |
| 5 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
 8”¢ČēĶ¼£¬Rt”÷AOBµÄŠ±±ßOAŌŚyÖįÉĻ£¬ĒŅOA=5£¬OB=4£®½«Rt”÷AOBČĘŌµćOÄꏱÕėŠż×ŖŅ»¶ØµÄ½Ē¶Č£¬Ź¹Ö±½Ē±ßOBĀäŌŚxÖįµÄøŗ°ėÖįÉĻµĆµ½ĻąÓ¦µÄRt”÷A”äOB”䣬ŌņA”äµćµÄ×ų±źŹĒ
8”¢ČēĶ¼£¬Rt”÷AOBµÄŠ±±ßOAŌŚyÖįÉĻ£¬ĒŅOA=5£¬OB=4£®½«Rt”÷AOBČĘŌµćOÄꏱÕėŠż×ŖŅ»¶ØµÄ½Ē¶Č£¬Ź¹Ö±½Ē±ßOBĀäŌŚxÖįµÄøŗ°ėÖįÉĻµĆµ½ĻąÓ¦µÄRt”÷A”äOB”䣬ŌņA”äµćµÄ×ų±źŹĒ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
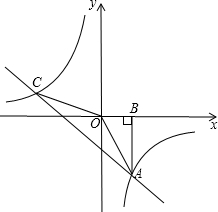 ČēĶ¼£¬Rt”÷AOBµÄ¶„µćAŹĒŅ»“ĪŗÆŹży=-x+£Øk+1£©µÄĶ¼ĻóÓė·“±ČĄżŗÆŹży=
ČēĶ¼£¬Rt”÷AOBµÄ¶„µćAŹĒŅ»“ĪŗÆŹży=-x+£Øk+1£©µÄĶ¼ĻóÓė·“±ČĄżŗÆŹży=| k |
| x |
| 3 |
| 2 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
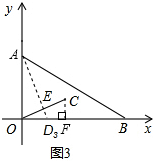
 £Ø2004•Ģ©°²£©ČēĶ¼£¬Rt”÷AOBµÄĮ½Ö±½Ē±ßOA”¢OBµÄ³¤·Ö±šŹĒ1ŗĶ3£¬½«”÷AOBČĘOµć°“ÄꏱÕė·½ĻņŠż×Ŗ90”ć£¬ÖĮ”÷DOCµÄĪ»ÖĆ£®
£Ø2004•Ģ©°²£©ČēĶ¼£¬Rt”÷AOBµÄĮ½Ö±½Ē±ßOA”¢OBµÄ³¤·Ö±šŹĒ1ŗĶ3£¬½«”÷AOBČĘOµć°“ÄꏱÕė·½ĻņŠż×Ŗ90”ć£¬ÖĮ”÷DOCµÄĪ»ÖĆ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
| 2 |
| 10 |
| 3 |
| 10 |
| 3 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com