
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).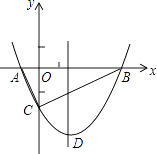
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
【答案】
(1)解:∵点A(﹣1,0)在抛物线y= ![]() x2+bx﹣2上,
x2+bx﹣2上,
∴ ![]() ×(﹣1 )2+b×(﹣1)﹣2=0,
×(﹣1 )2+b×(﹣1)﹣2=0,
解得:b=﹣ ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2.
x﹣2.
y= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴顶点D的坐标为:( ![]() ,﹣
,﹣ ![]() )
)
(2)解:当x=0时y=﹣2,∴C(0,﹣2),OC=2.
当y=0时, ![]() x2﹣
x2﹣ ![]() x﹣2=0,
x﹣2=0,
解得:x1=﹣1,x2=4,
∴B (4,0),
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形
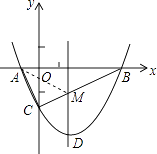
(3)解:如图所示:连接AM,
点A关于对称轴的对称点B,BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,
MC+MA的值最小,即△ACM周长最小,
设直线BC解析式为:y=kx+d,则 ![]() ,
,
解得:  ,
,
故直线BC的解析式为:y= ![]() x﹣2,
x﹣2,
当x= ![]() 时,y=﹣
时,y=﹣ ![]() ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
△ACM最小周长是:AC+AM+MC=AC+BC= ![]() +2
+2 ![]() =3
=3 ![]() .
.
【解析】(1)直接将(﹣1,0),代入解析式进而得出答案,再利用配方法求出函数顶点坐标;(2)分别得出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,进而利用勾股定理的逆定理得出即可;(3)利用轴对称最短路线求法得出M点位置,再求△ACM周长最小值.


科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条长1200 m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
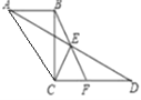
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D. 
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=5,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,连接AD,点E是AD的中点,连接BE并延长交CD于F点.
(1)请说明△ABE≌△DFE的理由;
(2)连接CB,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),交y轴于点C,点D是线段OB上一动点,连接CD,将CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF,CE交于点G.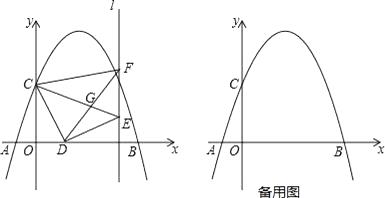
(1)求抛物线解析式;
(2)求线段DF的长;
(3)当DG= ![]() 时,
时,
①求tan∠CGD的值;
②试探究在x轴上方的抛物线上,是否存在点P,使∠EDP=45°?若存在,请写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
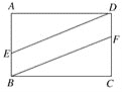
【题目】如图,长方形ABCD表示一块草地,点E,F分别在边AB、CD上,BF∥DE,四边形EBFD是一条水泥小路,若AD=12米,AB=7米,且AE∶EB=5∶2,求草地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com