
【题目】春节期间,为了满足百姓的消费需求,某商场计划购进冰箱、彩电进行销售.冰箱、彩电的进价、售价如表:
进价(元/台) | 售价(元/台) | |
冰箱 | M | 2500 |
彩电 | m﹣400 | 2000 |
(1)商场用80000元购进冰箱的数量用64000元购进彩电的数量相等,求表中m的值;
(2)为了满足市场需要要求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的![]() ;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
;若该商场将购进的冰箱、彩电全部售出,求能获得的最大利润w的值.
【答案】(1)m=2000;
(2)w的最大值为22500元.
【解析】
试题分析:(1)根据总价÷单价=数量由80000元购进冰箱的数量与用64000元购进彩电的数量相等建立方程求出其解即可;
(2)设购买彩电x台,则购进冰箱(50﹣x)台.用含x的代数式表示利润W,根据x的取值范围和一次函数的性质求解.
试题解析:(1)由题意,得![]() =
=![]() ,解得:m=2000,
,解得:m=2000,
经检验,m=2000是原方程的解,且符合题意.∴m=2000;
(2)设购买冰箱x台,则购买彩电(50﹣x)台,由题意,得
W=(2500﹣2000)x+(2000﹣1600)(50﹣x),
=100x+20000.
∵k=100>0,
∴W随x的增大而增大,
∴x=25时,W最大=22500,
∴w的最大值为22500元.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
A. a=1.5,b=2,c=3 B. a=7,b=24,c=25
C. a=6,b=8,c=10 D. a=0.3,b=0.4,c=0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,观察图象,回答问题:
(1)点D的纵坐标等于____.
(2)点A的横坐标是方程______的解.
(3)大于点B横坐标的x的值是不等式________的解.
(4)点C的横、纵坐标是方程组_________的解.
(5)小于点C横坐标的x的值是不等式__________的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①、②,解答下面各题:
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数.
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)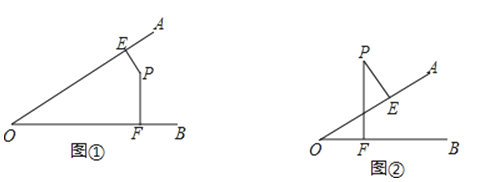
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论不正确的是( )
A.若a<0,b>0,则a-b<0
B.若a>0,b<0,则a-b>0
C.若a<0,b<0,则a-(-b)>0
D.若a<0,b<0,且|a|>|b|,则a-b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)20132﹣2012×2014(简便计算)
(3)(3a2)3+a2a4﹣a8÷a2
(4)(x﹣2)(3x﹣1)
(5)(x﹣1)(x+1)﹣(x+2)2
(6)(a+3b﹣2c)(a﹣3b﹣2c)
(7)(m﹣2n+1)2
(8)(2a﹣3b)2(2a+3b)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com