练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

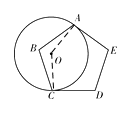
    【题目】如图，半径为1的⊙O与正五边形ABCDE相切于点A、C ， 则弧AC的长为

    A. π
    B. π
    C. π
    D. π

    【答案】C
    【解析】解：连接OA，OC，
    因为⊙O与正五边形ABCDE相切于点A、C ，
    所以∠OAE=∠OCD=90°，
    由多边形内角和公式可得正五边形的每个内角为（5-2）×180°÷5=108°，
    所以∠AOC=540°-∠OAE-∠AED-∠EDC-∠DCO=144°，
    则弧AC的长为.

    故选C.
    【考点精析】认真审题，首先需要了解正多边形的性质(正多边形都是轴对称图形．一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心;正多边形的中心边数为偶数的正多边形是中心对称图形，它的对称中心是正多边形的中心)，还要掌握多边形的对角线(设多边形的边数为n，则多边形的对角线条数为n(n-3)/2)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx的对称轴为x=，且经过点A（2，1），点P是抛物线上的动点，P的横坐标为m（0＜m＜2），过点P作PB⊥x轴，垂足为B，PB交OA于点C，点O关于直线PB的对称点为D，连接CD，AD，过点A作AE⊥x轴，垂足为E．

    （1）求抛物线的解析式;
    （2）填空：
    ①用含m的式子表示点C，D的坐标：
    C（　 ，　 　），D（　 ， ）；
    ②当m=　 　时，△ACD的周长最小；
    （3）若△ACD为等腰三角形，求出所有符合条件的点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°．若斜坡FA的坡比i=1： ，求大树的高度．（结果保留一位小数）参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11， 取1.73．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】快车和慢车同时从甲、乙两地出发开往乙地和甲地，匀速行驶，快车到达乙地后休息一个小时按原速返回，慢车在快车前一个小时到达甲地．如图表示慢车行驶过程中离甲地的路程y（km）与出发时间x（h）的函数图象，请结合图中的信息，解答下列问题：

    （1）甲、乙两地的距离为　 　km，慢车的速度为　 　km/h，快车的速度为　 　km/h；

    （2）在图①中画出快车离甲地的路程y（km）与出发时间x（h）的函数图象（坐标轴标注相关数值）；

    （3）求出发多长时间，两车相距150km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=15，AC=13，BC边上的高AD=12，则BC的长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

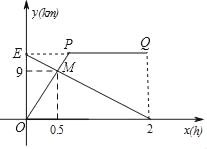
    【题目】甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图的折线OPQ和线段EF，分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x（h）之间的函数关系，且OP与EF相交于点M．

    （1）求线段OP对应的y甲与x的函数关系式（不必注明自变量x的取值范围）；

    （2）求y乙与x的函数关系式以及A，B两地之间的距离；

    （3）请从A，B两题中任选一题作答，我选择　 　题．

    A．直接写出经过多少小时，甲、乙两人相距3km；

    B．设甲、乙两人的距离为s（km），直接写出s与x的函数关系式，并注明x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】三角板是学习数学的重要工具，将一副三角板中的两块直角三角板的直角顶点按如图方式叠放在一起，当且点在直线的上方时，解决下列问题：（友情提示：，，．

    （1）①若，则的度数为　　；

    ②若，则的度数为　　；

    （2）由（1）猜想与的数量关系，并说明理由．

    （3）这两块三角板是否存在一组边互相平行？若存在，请直接写出的角度所有可能的值（不必说明理由）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答题
    （1）如图1，在正方形ABCD中，点O是对角线AC的中点，点E是边BC上一点，连接OE，过点O作OE的垂线交AB于点F．求证：OE=OF．
    （2）若将（1）中，“正方形ABCD”改为“矩形ABCD”，其他条件不变，如图2，连接EF． ⅰ）求证：∠OEF=∠BAC．
    ⅱ）试探究线段AF，EF，CE之间数量上满足的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A,B,C在同一直线上,线段AB=10cm且AC=6cm,M是AB的中点, N是AC的中点,则线段MN的长度是_________.

    查看答案和解析>>

    同步练习册答案