
【题目】如图,AB为⊙O的直径,点C、点D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,连接AC、AD、BC,若∠ABD=2∠BDC.
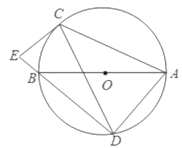
(1)求证:CE是⊙0的切线
(2)求证:△ABC![]() △CBE
△CBE
(3)若⊙O的半径为5,tan∠BDC=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)见解析;(3)2
【解析】
(1)连接OC,可证明OC∥DE,由于CE⊥DB,∠CED=90°,所以∠OCE=90°,OC⊥CE,根据切线的判定即可求出答案;
(2)由AB是⊙O的直径,可得![]() ,可得
,可得![]() ,再证∠ECB=∠CAB,即可得出结论;
,再证∠ECB=∠CAB,即可得出结论;
(3)连接BC,由于∠BDC=∠BAC,所以![]() ,设BC=x,AC=2x,所以
,设BC=x,AC=2x,所以![]() ,列出方程即可求出x的值,利用△ABC
,列出方程即可求出x的值,利用△ABC![]() △CBE可求出BE的长度.
△CBE可求出BE的长度.
(1)证明:连接![]()

∵![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵OC为![]() 的半径
的半径
∴![]() 是
是![]() 的切线
的切线
(2)连接![]()

∵AB是⊙O的直径
∴![]()
∴![]()
∵∠ECO=∠BCA=90°
∴∠ECB+∠BCO=∠OCA+∠BCO
∴∠ECB=∠OCA
∵![]()
∴∠ECB=∠CAB
∴△ABC![]() △CBE
△CBE
(3)∵![]() ,
,
∴![]()
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
设![]() ,
,![]()
∴![]()
∵![]() 的半径为5
的半径为5
∴![]()
∴![]()
∴![]()
∵△ABC![]() △CBE
△CBE
∴![]()
∴![]()
∴BE=2


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
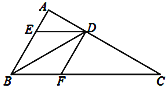
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
⑴求证:四边形BEDF为菱形;
⑵如果∠A=100°,∠C=30°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学测量树的高度时,发现树的影子有一部分0.2米落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是4.62米”;小强说:“要是没有台阶遮挡的话,树的影子长度肯定比4.62米要长”.

(1)你认为小玲和小强的说法对吗?
(2)请根据小玲和小强的测量数据计算树的高度;
(3)要是没有台阶遮挡的话,树的影子长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
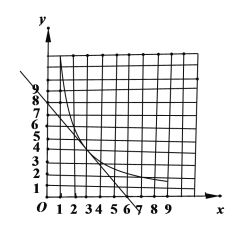
(1)填空:反比例函数的解析式为____________________,直线AC的解析式为____________________,B点的坐标是________.
(2)在平面内有点D,使得以A,B,C,D四点为项点的边形为平行四边形.
①在图中用直尺和2B铅笔画出所有符合条件的平行四边形;
②根据所画形,请直接写出符合条件的所有点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
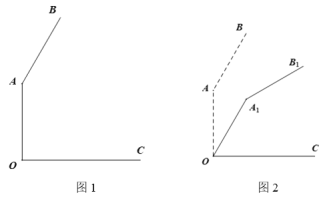
【题目】图1是某品牌台灯竖直摆放在水平桌面上的侧面示意图,其中![]() 为桌面(台灯底座的厚度忽略不计),台灯支架
为桌面(台灯底座的厚度忽略不计),台灯支架![]() 与灯管
与灯管![]() 的长度都为
的长度都为![]() ,且夹角为
,且夹角为![]() (即
(即![]() ),若保持该夹角不变,当支架
),若保持该夹角不变,当支架![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 时,支架与灯管落在
时,支架与灯管落在![]() 位置(如图2所示),则灯管末梢
位置(如图2所示),则灯管末梢![]() 的高度会降低_______
的高度会降低_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
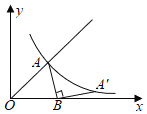
【题目】如图,函数y=x(x≥0)的图象与反比例函数y=![]() 的图象交于点A,若点A绕点B(
的图象交于点A,若点A绕点B(![]() ,0)顺时针旋转90°后,得到的点A'仍在y=
,0)顺时针旋转90°后,得到的点A'仍在y=![]() 的图象上,则点A的坐标为_____.
的图象上,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线表达式C:![]() , 已知点A(0,2),点P是抛物线上一点,若Rt△AOP有一个锐角正切值为
, 已知点A(0,2),点P是抛物线上一点,若Rt△AOP有一个锐角正切值为![]() ,则点P的坐标_________________.
,则点P的坐标_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
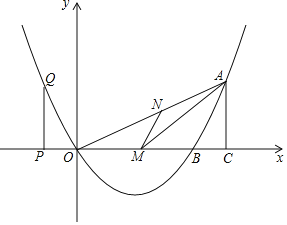
【题目】如图,已知二次函数的图象过点O(0,0).A(8,4),与x轴交于另一点B,且对称轴是直线x=3.
(1)求该二次函数的解析式;
(2)若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求M的坐标;
(3)P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q.过A作AC⊥x轴于C,当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
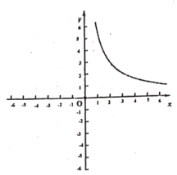
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是除0外的全体实数,
的取值范围是除0外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 1 | 2 | 3 | 6 | … |
| … | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | … |
其中,![]() _________.
_________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出一条函数性质.
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________.
的实数根的情况是________.
②方程![]() 有_______个实效根;
有_______个实效根;
③关于![]() 的方程
的方程![]() 有2个实数根,
有2个实数根,![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com