
дФЖСРэНтЃКЖдгкШЮвте§ЪЕЪ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ ![]() ЃЌжЛгаЕу
ЃЌжЛгаЕу![]() ЪБЃЌЕШКХГЩСЂЃЎ
ЪБЃЌЕШКХГЩСЂЃЎ
НсТлЃКдк![]() ЃЈ
ЃЈ![]() ОљЮЊе§ЪЕЪ§ЃЉжаЃЌШє
ОљЮЊе§ЪЕЪ§ЃЉжаЃЌШє![]() ЮЊЖЈжЕ
ЮЊЖЈжЕ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
жЛгаЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕ
газюаЁжЕ![]() ЃЎ
ЃЎ
ИљОнЩЯЪіФкШнЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉШє![]() ЃЌжЛгаЕБ
ЃЌжЛгаЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюаЁжЕ ЃЎ
газюаЁжЕ ЃЎ
ЃЈ2ЃЉЫМПМбщжЄЃКШчЭМЃЌ![]() ЮЊАыдВ
ЮЊАыдВ![]()
![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЮЊАыдВЩЯШЮвтвЛЕуЃЌЃЈгыЕу
ЮЊАыдВЩЯШЮвтвЛЕуЃЌЃЈгыЕу![]() ВЛжиКЯЃЉЃЎЙ§Еу
ВЛжиКЯЃЉЃЎЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
гУa,bЕФДњЪ§ЪНБэЪОCDЁЃ
‚ЪдИљОнЭМаЮбщжЄ![]() ЃЌВЂжИГіЕШКХГЩСЂЪБЕФЬѕМўЃЎ
ЃЌВЂжИГіЕШКХГЩСЂЪБЕФЬѕМўЃЎ


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
 ЮЪРИИЫЖрЩйГЄЪБЃЌЫљгУРСІFзюаЁЃПЪЧЖрЩйЃП
ЮЪРИИЫЖрЩйГЄЪБЃЌЫљгУРСІFзюаЁЃПЪЧЖрЩйЃПВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
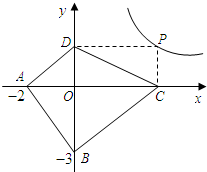 дФЖСРэНтЃКЖдгкШЮвте§ЪЕЪ§aЃЌbЃЌ
дФЖСРэНтЃКЖдгкШЮвте§ЪЕЪ§aЃЌbЃЌ| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 4 |
| x |
| 6 |
| x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
| a |
| b |
| ab |
| ab |
| P |
| P |
| ab |

| 1 |
| m |
| 12 |
| x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКдФЖСРэНт
 дФЖСРэНтЃК
дФЖСРэНтЃК| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| 12 |
| x |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com