
【题目】如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=![]() x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
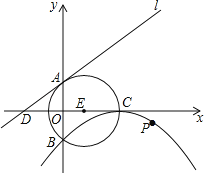
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
【答案】(1)y=-![]() x2+x-4;(2)直线l与⊙E相切与A.(3) 抛物线上的动点P的坐标为(2,-
x2+x-4;(2)直线l与⊙E相切与A.(3) 抛物线上的动点P的坐标为(2,-![]() )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为![]() .
.
【解析】
试题分析:(1)连接AE,由已知得:AE=CE=5,OE=3,利用勾股定理求出OA的长,结合垂径定理求出OC的长,从而得到C点坐标,进而得到抛物线的解析式;
(2)求出点D的坐标为(-![]() ,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
,0),根据△AOE∽△DOA,求出∠DAE=90°,判断出直线l与⊙E相切与A.
(3)过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.设M(m,![]() m+4),P(m,-
m+4),P(m,-![]() m2+m-4),得到PM=
m2+m-4),得到PM=![]() m+4-(-
m+4-(-![]() m2+m-4)=
m2+m-4)=![]() m2-
m2-![]() m+8=
m+8=![]() (m-2)2+
(m-2)2+![]() ,根据△PQM的三个内角固定不变,得到PQ最小=PM最小
,根据△PQM的三个内角固定不变,得到PQ最小=PM最小![]() sin∠QMP=PM最小
sin∠QMP=PM最小![]() sin∠AEO=
sin∠AEO=![]() ×
×![]() =
=![]() ,从而得到最小距离.
,从而得到最小距离.
试题解析:(1)如图1,连接AE,由已知得:AE=CE=5,OE=3,
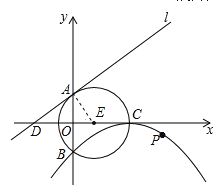
在Rt△AOE中,由勾股定理得,OA=![]() ,
,
∵OC⊥AB,
∴由垂径定理得,OB=OA=4,
OC=OE+CE=3+5=8,
∴A(0,4),B(0,-4),C(8,0),
∵抛物线的顶点为C,
∴设抛物线的解析式为y=a(x-8)2,
将点B的坐标代入上解析的式,得64a=-4,故a=-![]() ,
,
∴y=-![]() (x-8)2,
(x-8)2,
∴y=-![]() x2+x-4为所求抛物线的解析式,
x2+x-4为所求抛物线的解析式,
(2)在直线l的解析式y=![]() x+4中,令y=0,得
x+4中,令y=0,得![]() x+4=0,解得x=-
x+4=0,解得x=-![]() ,
,
∴点D的坐标为(-![]() ,0),
,0),
当x=0时,y=4,
∴点A在直线l上,
在Rt△AOE和Rt△DOA中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵∠AOE=∠DOA=90°,
∴△AOE∽△DOA,
∴∠AEO=∠DAO,
∵∠AEO+∠EAO=90°,
∴∠DAO+∠EAO=90°,即∠DAE=90°,因此,直线l与⊙E相切与A.
(3)如图2,过点P作直线l的垂线段PQ,垂足为Q,过点P作直线PM垂直于x轴,交直线l于点M.

设M(m,![]() m+4),P(m,-
m+4),P(m,-![]() m2+m-4),则
m2+m-4),则
PM=![]()
![]() m+4-(-
m+4-(-![]() m2+m-4)=
m2+m-4)=![]() m2-
m2-![]() m+8=
m+8=![]() (m-2)2+
(m-2)2+![]() ,
,
当m=2时,PM取得最小值![]() ,
,
此时,P(2,-![]() ),
),
对于△PQM,
∵PM⊥x轴,
∴∠QMP=∠DAO=∠AEO,
又∠PQM=90°,
∴△PQM的三个内角固定不变,
∴在动点P运动的过程中,△PQM的三边的比例关系不变,
∴当PM取得最小值时,PQ也取得最小值,
PQ最小=PM最小![]() sin∠QMP=PM最小
sin∠QMP=PM最小![]() sin∠AEO=
sin∠AEO=![]() ×
×![]() =
=![]() ,
,
∴当抛物线上的动点P的坐标为(2,-![]() )时,点P到直线l的距离最小,其最小距离为
)时,点P到直线l的距离最小,其最小距离为![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
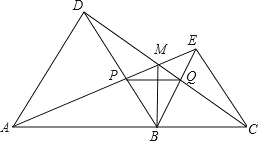
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A,B两点(点A在点B左侧),与y轴交于点C,点A,C的坐标分别为(-3,0),(0,3),对称轴直线x=-1交x轴于点E,点D为顶点.
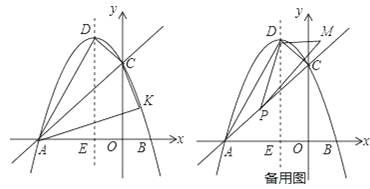
(1)求抛物线的解析式;
(2)点K是直线AC下方的抛物线上一点,且S△KAC=S△DAC求点K的坐标;
(3)如图2若点P是线段AC上的一个动点,∠DPM=30°,DP⊥DM,则点P的线段AC上运动时,D点不变,M点随之运动,求当点P从点A运动到点C时,点M运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
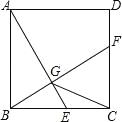
【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为![]() -1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
-1.其中正确的说法是 .(把你认为正确的说法的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com