
 如图,已知EC∥AB,∠EDA=∠ABF.
如图,已知EC∥AB,∠EDA=∠ABF.分析 (1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形;
(2)根据平行相似可以得三角形相似;
(3)由EC∥AB,可得$\frac{OA}{OE}=\frac{OB}{OD}$,由AD∥BC,可得$\frac{OB}{OD}=\frac{OF}{OA}$,等量代换得出$\frac{OA}{OE}=\frac{OF}{OA}$,可得结论.
解答 证明:(1)∵EC∥AB,
∴∠EDA=∠DAB,
∵∠EDA=∠ABF,
∴∠DAB=∠ABF,
∴AD∥BC,
∵DC∥AB,
∴四边形ABCD为平行四边形;
(2)存在6对三角形相似,分别是:
①∵EC∥AB,
∴△ABF∽△ECF;
②由(1)知:AD∥BC,
∴△EDA∽△ECF;
③∵△ABF∽△ECF,△EDA∽△ECF,
∴△ABF∽△EDA;
④∵四边形ABCD为平行四边形,
∴△ADB∽△CBD;
⑤∵EC∥AB,
∴△OAB∽△OED;
⑥∵AD∥BC,
∴△OBF∽△ODA;
(3)∵EC∥AB,
∴△OAB∽△OED,
∴$\frac{OA}{OE}=\frac{OB}{OD}$,
∵AD∥BC,
∴△OBF∽△ODA,
∴$\frac{OB}{OD}=\frac{OF}{OA}$,
∴$\frac{OA}{OE}=\frac{OF}{OA}$,
∴OA2=OE•OF.
点评 此题考查了相似三角形的判定与性质,平行四边形的判定,平行线的性质,解题时要注意识图,灵活应用数形结合思想.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
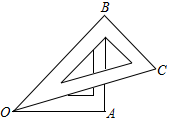 如图,将一副三角板摆放在一起
如图,将一副三角板摆放在一起查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com