
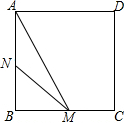
 如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )| A. | 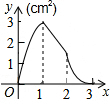 | B. | 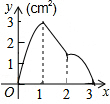 | C. | 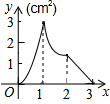 | D. | 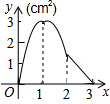 |
分析 分三种情况进行讨论,当0≤x≤1时,当1≤x≤2时,当2≤x≤3时,分别求得△ANM的面积,列出函数解析式,根据函数图象进行判断即可.
解答 解:由题可得,BN=x,
当0≤x≤1时,M在BC边上,BM=3x,AN=3-x,则
S△ANM=$\frac{1}{2}$AN•BM,
∴y=$\frac{1}{2}$•(3-x)•3x=-$\frac{3}{2}$x2+$\frac{9}{2}$x,故C选项错误;
当1≤x≤2时,M点在CD边上,则
S△ANM=$\frac{1}{2}$AN•BC,
∴y=$\frac{1}{2}$(3-x)•3=-$\frac{3}{2}$x+$\frac{9}{2}$,故D选项错误;
当2≤x≤3时,M在AD边上,AM=9-3x,
∴S△ANM=$\frac{1}{2}$AM•AN,
∴y=$\frac{1}{2}$•(9-3x)•(3-x)=$\frac{3}{2}$(x-3)2,故B选项错误;
故选(A).
点评 本题主要考查了动点问题的函数图象,用图象解决问题时,要理清图象的含义即会识图.利用数形结合,分类讨论是解决问题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
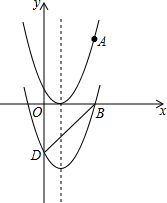 如图,抛物线C1:y=a(x-1)2经过点A(3,4).
如图,抛物线C1:y=a(x-1)2经过点A(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
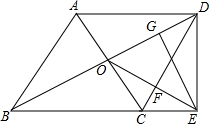 如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.
如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
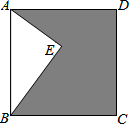 如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )
如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是( )| A. | 76 | B. | 24 | C. | 48 | D. | 88 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com