
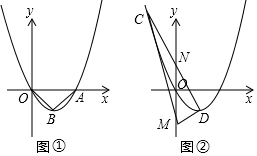
���� ��1���������֪B��1��-1����A��2��0�������ô���ϵ�������ɽ�����⣮
��2���������M��ֱ�ߵĽ���ʽΪy=kx-1����$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}-2x}\end{array}\right.$��ȥy�õ�x2-��2+k��x+1=0�����ݡ�=0ʱ���k=-4��0�������C��D�������꼴�ɽ�����⣮
�ڽ��ۣ�OM=ON����M��0��-t2��������M��ֱ�ߵĽ���ʽΪy=kx-t2����$\left\{\begin{array}{l}{y=kx-{t}^{2}}\\{y={x}^{2}-2x}\end{array}\right.$��ȥy�õ�x2-��2+k��x+t2=0���������=0ʱ����2+k��2-4t2=0��
���k=2t-2��-2t-2�������C��D�������꣬���ݶԳ��Լ��ɽ�����⣮
��� �⣺��1����������y=a��x-1��2+k������ԭ�㣬����ΪB����x������һ��A���ҡ�OABΪ����ֱ�������Σ�
��Գ���x=1��A��2��0����B��1��-1����
��k=-1��
�������ߵĽ���ʽΪy=a��x-1��2-1����A��2��0�������a=1��
�������ߵĽ���ʽΪy=x2-2x��
��2���������M��ֱ�ߵĽ���ʽΪy=kx-1��
��$\left\{\begin{array}{l}{y=kx-1}\\{y={x}^{2}-2x}\end{array}\right.$����ȥy�õ�x2-��2+k��x+1=0��
�������=0ʱ����2+k��2-4=0�����k=-4��0��
k=-4ʱ����$\left\{\begin{array}{l}{y=-4x-1}\\{y={x}^{2}-2x}\end{array}\right.$�����$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$��
��C��-1��3����
k=0ʱ��ֱ��DM��x�ᣬD��1��-1����
��C��-1��3����D��1��-1����
���N���߶�CD���е㣬N��0��1����
�ڽ��ۣ�OM=ON��
���ɣ���M��0��-t2��������M��ֱ�ߵĽ���ʽΪy=kx-t2��
��$\left\{\begin{array}{l}{y=kx-{t}^{2}}\\{y={x}^{2}-2x}\end{array}\right.$��ȥy�õ�x2-��2+k��x+t2=0��
�������=0ʱ����2+k��2-4t2=0��
���k=2t-2��-2t-2��
��$\left\{\begin{array}{l}{y=��2t-2��x-{t}^{2}}\\{y={x}^{2}-2x}\end{array}\right.$���$\left\{\begin{array}{l}{x=t}\\{y={t}^{2}-2t}\end{array}\right.$��
��$\left\{\begin{array}{l}{y=��-2t-2��x-{t}^{2}}\\{y={x}^{2}-2x}\end{array}\right.$���$\left\{\begin{array}{l}{x=-t}\\{y={t}^{2}+2t}\end{array}\right.$��
������C��t��t2-2t����D��-t��t2+2t����
��C��D����ĺ����껥Ϊ�෴����
��NC=ND��
��N��0��t2����
��OM=ON=t2��
��OM=ON��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á���Ԫ���η����飬һԪ���η��̵ĸ����б�ʽ��֪ʶ������Ĺؼ��ǰ���������ͼ��Ľ������⣬ת��ΪһԪ���η��̵ĸ��ĸ������⣬���ø����б�ʽ�������������⣬ѧ�����ò���������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
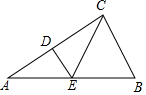 �ڡ�ABC�У�DE��ֱƽ��AC��AB�ڵ�E����A=30�㣬��BCE=50�㣬���B=��������
�ڡ�ABC�У�DE��ֱƽ��AC��AB�ڵ�E����A=30�㣬��BCE=50�㣬���B=��������| A�� | 60�� | B�� | 70�� | C�� | 80�� | D�� | 50�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
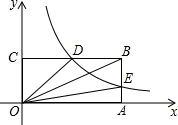 ��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬����OABC�ı�OA��OC�ֱ���x���y���ϣ�����OA=6��OC=3����֪����������y=$\frac{k}{x}$��x��0����ͼ��BC���ϵ��е�D����AB�ڵ�E��
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬����OABC�ı�OA��OC�ֱ���x���y���ϣ�����OA=6��OC=3����֪����������y=$\frac{k}{x}$��x��0����ͼ��BC���ϵ��е�D����AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
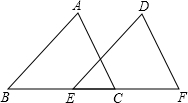 ��ͼ���ڡ�ABC�͡�DEF�У���B=��DEF��AB=DE����������һ����������Ȼ����֤����ABC�ա�DEF����������ǣ�������
��ͼ���ڡ�ABC�͡�DEF�У���B=��DEF��AB=DE����������һ����������Ȼ����֤����ABC�ա�DEF����������ǣ�������| A�� | ��A=��D | B�� | BE=FC | C�� | ��ACB=��F | D�� | AC=DF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��2����B��1��3������AOB����y��ԳƵ�ͼ��Ϊ��A1OB1��
��ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ���A��B������ֱ���A��3��2����B��1��3������AOB����y��ԳƵ�ͼ��Ϊ��A1OB1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ע��6�����й��У�1��ͬλ�ǣ�3���ڴ��ǣ�4��ͬ���ڽǣ���ͼ���й���3��ͬ���ڽǣ�
��ͼ������ע��6�����й��У�1��ͬλ�ǣ�3���ڴ��ǣ�4��ͬ���ڽǣ���ͼ���й���3��ͬ���ڽǣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com