
【题目】在平面直角坐标系![]() 中,已知P(
中,已知P(![]() ,
,![]() ),R(
),R(![]() ,
,![]() )两点,且
)两点,且![]() ,
,![]() ,若过点P作
,若过点P作![]() 轴的平行线,过点R作
轴的平行线,过点R作![]() 轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作
轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作![]() 轴的平行线,过点P作
轴的平行线,过点P作![]() 轴的平行线,两平行线交于一点
轴的平行线,两平行线交于一点![]() ,连接PR,则称△RP
,连接PR,则称△RP![]() 为点R,P,
为点R,P,![]() 的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.
的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.

(1)已知点A(0,4),点B(3,0),若△ABC是点A,B,C的“坐标轴三角形”,则点C的坐标为 ;
(2)已知点D(2,1),点E(e,4),若点D,E,F的“坐标轴三角形”的面积为3,求e的值.
(3)若![]() 的半径为
的半径为![]() ,点M(
,点M(![]() ,4),若在
,4),若在![]() 上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求
上存在一点N,使得点N,M,G的“坐标轴三角形”为等腰三角形,求![]() 的取值范围.
的取值范围.
【答案】(1)(3,4);(2)![]() 或
或![]() ;(3)m的取值范围是
;(3)m的取值范围是![]() 或
或![]() .
.
【解析】
(1)根据点C到x轴、y轴的距离解答即可;
(2)根据“坐标轴三角形”的定义求出线段DF和EF,然后根据三角形的面积公式求解即可;
(3)根据题意可得:符合题意的直线MN应为y=x+b或y=-x+b.①当直线MN为y=x+b时,结合图形可得直线MN平移至与⊙O相切,且切点在第四象限时,b取得最小值,根据等腰直角三角形的性质和勾股定理可求得b的最小值,进而可得m的最大值;当直线MN平移至与⊙O 相切,且切点在第二象限时,b取得最大值,根据等腰直角三角形的性质和勾股定理可求得b的最大值,进而可得m的最小值,可得m的取值范围;②当直线MN为y=-x+b时,同①的方法可得m的另一个取值范围,问题即得解决.
解:(1)根据题意作图如下:

由图可知:点C到x轴距离为4,到y轴距离为3,∴C(3,4);
故答案为:(3,4);
(2) ∵点D(2,1),点E(e,4),点D,E,F的“坐标轴三角形”的面积为3,
∴![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() =2,解得:e=4或e=0;
=2,解得:e=4或e=0;
(3)由点N,M, G的“坐标轴三角形”为等腰三角形可得:直线MN为y=x+b或y=-x+b.
①当直线MN为y=x+b时,由于点M的坐标为(m,4),可得m=4-b,
由图可知:

当直线MN平移至与⊙O相切,且切点在第四象限时,b取得最小值.
此时直线MN记为M1 N1,其中N1为切点,T1为直线M1 N1与y轴的交点.
∵△O N1T1为等腰直角三角形,ON=![]() ,∴
,∴![]() ,
,
∴b的最小值为-3,∴m的最大值为m=4-b=7;
当直线MN平移至与⊙O 相切,且切点在第二象限时,b取得最大值.
此时直线MN记为M2 N2,其中N2为切点,T2为直线M2 N2与y轴的交点.
∵△ON2T为等腰直角三角形,ON2=![]() ,∴
,∴![]() ,
,
∴b的最大值为3,∴m的最小值为m=4-b=1,
∴m的取值范围是![]() ;
;
②当直线MN为y=-x+b时,同理可得,m=b-4,
当b=3时,m=-1;当b=-3时,m=-7;
∴m的取值范围是![]() .
.
综上所述,m的取值范围是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转 270°后得到扇形COD,AP,BQ分别切优弧CD于点P,Q,且点P,Q在AB异侧,连接OP.
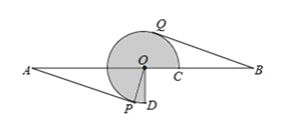
(1)求证:AP=BQ;
(2)当BQ= ![]() 时,求
时,求![]() 的长(结果保留
的长(结果保留 ![]() );
);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE=________,EF=__________
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.(![]() 相遇时除外)
相遇时除外)
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
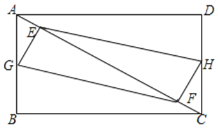
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点P是
是直径AB所对的半圆弧,点P是![]() 与直径AB所围成图形的外部的一个定点,AB=8cm,点C是
与直径AB所围成图形的外部的一个定点,AB=8cm,点C是![]() 上一动点,连接PC交AB于点D.
上一动点,连接PC交AB于点D.
小明根据学习函数的经验,对线段AD,CD,PD,进行了研究,设A,D两点间的距离为x cm,C,D两点间的距离为![]() cm,P,D两点之间的距离为
cm,P,D两点之间的距离为![]() cm.
cm.

小明根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量x的变化而变化的规律进行了探究.
随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0.00 | 1.00 | 2.00 | 3.00 | 3.20 | 4.00 | 5.00 | 6.00 | 6.50 | 7.00 | 8.00 |
| 0.00 | 1.04 | 2.09 | 3.11 | 3.30 | 4.00 | 4.41 | 3.46 | 2.50 | 1.53 | 0.00 |
| 6.24 | 5.29 | 4.35 | 3.46 | 3.30 | 2.64 | 2.00 | m | 1.80 | 2.00 | 2.65 |
补充表格;(说明:补全表格时,相关数值保留两位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点,并画出函数
中,描出补全后的表中各组数值所对应的点,并画出函数![]() 的图象:
的图象:

(3)结合函数图象解决问题:当AD=2PD 时,AD的长度约为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.

(1)求证:AC是⊙O的切线;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子.
(1)如果果园既要让橙子的总产量达到60375个,又要确保每一棵橙子树接受到的阳光照射尽量少受影响,那么应该多种多少棵橙子树?
(2)增种多少棵橙子树,可以使果园橙子的总产量最多?最多为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是方城县潘河的某一段,现要估算河的宽度(即河两岸相对的两点A、B间的距离),可以按如下步骤操作:①先在河的对岸选定一个目标作为点A;②再在河的这一边选定点B和点C,使AB⊥BC;③再选定点E,使EC⊥BC,然后用视线确定BC和AE的交点D.
(1)用皮尺测得BC=177米,DC=61米,EC=50米,求河的宽度AB;(精确到0.1米)
(2)请用所学过的知识设计一种测量旗杆高度AB的方案.
要求:①画出示意图,所测长度用a、b、c等表示,直接标注在图中线段上;
②不要求写操作步骤;③结合所测数据直接用含a、b、c等字母的式子表示出旗杆高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
的图象与直线y2=3x-5相交于A(2,m),B(n,-6)两点.
(1)求反比例函数的表达式;
(2) 当y1﹥y2﹥0时,请直接写出x的取值范围;
(3)连接OA,OB,求△AOB的面积.
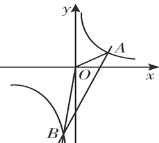
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com