
【题目】如图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,
(1)图中EC、BF有怎样的数量和位置关系?试证明你的结论.
(2)连接AM,求证:MA平分∠EMF.

【答案】(1)结论:EC=BF,EC⊥BF.理由详见解析;(2)详见解析.
【解析】
(1)先由条件可以得出∠EAC=∠BAE,再证明△EAC≌△BAF就可以得出结论;
(2)作AP⊥CE于P,AQ⊥BF于Q.由△EAC≌△BAF,推出AP=AQ(全等三角形对应边上的高相等).由AP⊥CE于P,AQ⊥BF于Q,可得AM平分∠EMF.
(1)结论:EC=BF,EC⊥BF,
理由:∵AE⊥AB,AF⊥AC,
∴∠EAB=∠CAF=90°,
∴∠EAB+∠BAC=∠CAF+∠BAC,
∴∠EAC=∠BAE,
在△EAC和△BAF中,
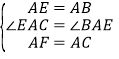 ,
,
∴△EAC≌△BAF(SAS),
∴EC=BF.∠AEC=∠ABF
∵∠AEG+∠AGE=90°,∠AGE=∠BGM,
∴∠ABF+∠BGM=90°,
∴∠EMB=90°,
∴EC⊥BF.
∴EC=BF,EC⊥BF;
(2)作AP⊥CE于P,AQ⊥BF于Q,
∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等)
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.


科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,![]() ,
,![]() ,
,![]() ,
,![]() ,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.
,动点M从B点出发沿线段BC以每秒2个单位长度的速度向C运动;动点N同时从A点出发沿线段AB以每秒1个单位长度的速度向B运动,其中一点到达终点时,则两点同时停止运动.设运动的时间为t秒,当△MNB为等腰直角三角形时,t的值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
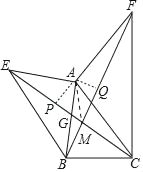
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
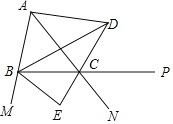
【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°.其中正确的结论有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一抛物线形大门,其地面宽度![]() .一同学站在门内,在离门脚
.一同学站在门内,在离门脚![]() 点
点![]() 远的
远的![]() 处,垂直地面立
处,垂直地面立
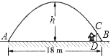
起一根![]() 长的木杆,其顶端恰好顶在抛物线形门上
长的木杆,其顶端恰好顶在抛物线形门上![]() 处.根据这些条件,请你求出该大门的高
处.根据这些条件,请你求出该大门的高![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
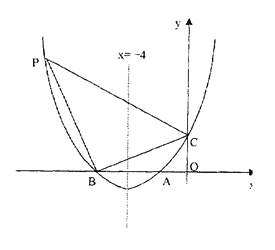
【题目】如图,已知抛物线的对称轴是x=-4,抛物线与x轴交于A,B两点,与y轴交于C点,O是坐标原点,且A,C的坐标分别是(-2,0),(0,3).
(1)求抛物线的解析式;
(2)抛物线上有一点是P,满足∠PBC=90,求P点的坐标;
(3)y轴上是否存在点E使得△AOE与△PBC相似?若存在求出点E的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com