
【题目】已知△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=6.
,BC=6.
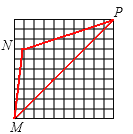
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点
的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需
证明).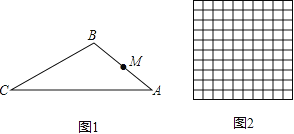
【答案】解:(1)①如图A,过点M作MN∥BC交AC于点N,
则△AMN∽△ABC,
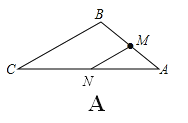
∵M为AB中点,∴MN是△ABC 的中位线。
∵BC=6,∴MN=3。
②如图B,过点M作∠AMN=∠ACB交AC于点N,
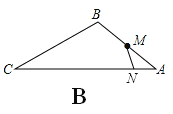
则△AMN∽△ACB,∴![]() 。
。
∵BC=6,AC=![]() ,AM=
,AM=![]() ,∴
,∴![]() ,解得MN=
,解得MN=![]() 。
。
综上所述,线段MN的长为3或![]() 。
。
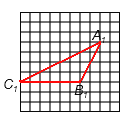
(2)①如图所示:
②每条对角线处可作4个三角形与原三角形相似,那么共有8个。
【解析】
网格问题,作图(相似变换),三角形中位线定理,相似三角形的性质。
(1)作MN∥BC交AC于点N,利用三角形的中位线定理可得MN的长;作∠AMN=∠B,利用相似可得MN的长。
(2)①A1B1=![]() 为直角三角形斜边的两直角边长为2,4,A1C1=
为直角三角形斜边的两直角边长为2,4,A1C1=![]() 为直角三角形斜边的两直角边长为4,8。以此,先作B1C1=6,画出△A1B1C1。
为直角三角形斜边的两直角边长为4,8。以此,先作B1C1=6,画出△A1B1C1。
②以所给网格的对角线作为原三角形中最长的边,可得每条对角线处可作4个三角形与原三角形相似,那么共有8个。


科目:初中数学 来源: 题型:
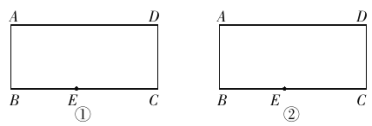
【题目】在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]
(1)在图①中,画∠BAD的平分线;
(2)在图②中,画∠BCD的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
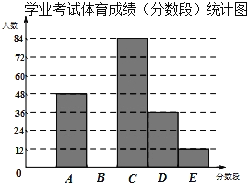
【题目】为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分)统计如下:
学业考试体育成绩(分数段)统计表
分数段 | 人数(人) | 频率 |
A | 48 | 0.2 |
B | a | 0.25 |
C | 84 | 0.35 |
D | 36 | b |
E | 12 | 0.05 |
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数.”请问:甲同学的体育成绩应在什么分数段内? (填相应分数段的字母)
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )

A. 10 B. 20 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
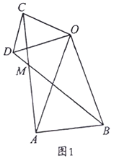
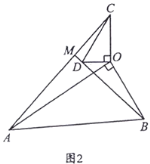
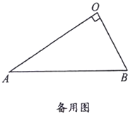
【题目】(1)如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=50°,连接AC,BD
交于点M.
①![]() 的值为 ;②∠AMB的度数为 °;
的值为 ;②∠AMB的度数为 °;
(2)如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.求![]() 的值及∠AMB的度数;
的值及∠AMB的度数;
(3)在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M.若OD=![]() ,OB=
,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com