
分析 (1)根据“总利润=每件的利润×每月销售量”得出函数解析式,配方成顶点式即可得出答案;
(2)根据每月获得的利润不低于2000元及销售单价不得高于32元求得x的取值范围,由总成本=每件成本×销售量得出函数解析式,根据一次函数的性质可得答案.
解答 解:(1)由题意,得:
w=(x-20)•y
=(x-20)•(-10x+500)
=-10x2+700-10000
=-10(x-35)2+2250,
答:当销售单价定为35元时,每月可获得最大利润;
(2)由题意,得:-10x2+700x-10000=2000,
解得:x1=30,x2=40,
∵a=-10<0,
∴抛物线开口向下,
∴当30≤x≤40时,w≥2000,
∵x≤32,
∴当30≤x≤32时,w≥2000,
设成本为P(元),由题意,得:
∵P=20(-10x+500)=-200x+10000,
∵k=-200<0,
∴P随x的增大而减小,
∴当x=32时,P最小=3600,
答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.
点评 本题主要考查二次函数的应用,理解题意由相等关系列出函数解析式,并由函数性质得出函数的最值是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
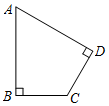 已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.
已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AB=AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com