
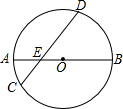
 如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,
如图,AB是⊙O的直径切AB=8,CD是弦,CD交AB于E,且E为OA的中点,∠BED=45°,分析 (1)作OF⊥CD于F,连结OD,如图,根据垂径定理得到CF=DF,易得OE=2,在Rt△OEF中利用等腰直角三角形的性质得OF=EF=$\frac{\sqrt{2}}{2}$OE=$\sqrt{2}$,再利用勾股定理得DF=$\sqrt{14}$,则CF=$\sqrt{14}$,所以CE2+DE2=(CF-EF)2+(DF+EF)2=2CF2+2EF2=32;
(2)设OE=a,与(1)一样可得OF=EF=$\frac{\sqrt{2}}{2}$OE=$\frac{\sqrt{2}}{2}$a,则DF=$\sqrt{16-\frac{1}{2}{a}^{2}}$,CF=$\sqrt{16-\frac{1}{2}{a}^{2}}$,所以CE2+DE2=(CF-EF)2+(DF+EF)2=2CF2+2EF2=32.
解答 解:(1)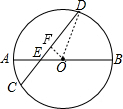 作OF⊥CD于F,连结OD,如图,则CF=DF,
作OF⊥CD于F,连结OD,如图,则CF=DF,
∵AB=8,E为OA的中点,
∴OE=2,
在Rt△OEF中,∵∠BED=45°,
∴OF=EF=$\frac{\sqrt{2}}{2}$OE=$\sqrt{2}$,
在Rt△ODF中,DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\sqrt{14}$,
∴CF=$\sqrt{14}$,
∴CE2+DE2=(CF-EF)2+(DF+EF)2=2CF2+2EF2=2×14+2×2=32;
(2)CE2+DE2的值不发生变化.
设OE=a,则OF=EF=$\frac{\sqrt{2}}{2}$OE=$\frac{\sqrt{2}}{2}$a,
在Rt△ODF中,DF=$\sqrt{O{D}^{2}-O{F}^{2}}$=$\sqrt{16-\frac{1}{2}{a}^{2}}$
∴CF=$\sqrt{16-\frac{1}{2}{a}^{2}}$,
∴CE2+DE2=(CF-EF)2+(DF+EF)2=2CF2+2EF2=2×(16-$\frac{1}{2}$a2)+2×$\frac{1}{2}$a2=32.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
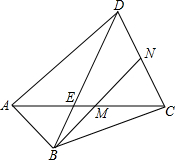 如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.
如图,在四边形ABCD中,△ABD,△BCD,△ABC的面积比是3:4:1,点M,N分别在AC,CD上,满足AM:AC=CN:CD,并且B,M,N共线.求证:M与N分别是AC和CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-8,4) | C. | (-8,4)或(8,-4) | D. | (-2,1)或(2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com