
【题目】如图所示,在直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 在原点,
在原点,![]() .若矩形以每秒2个单位长度沿
.若矩形以每秒2个单位长度沿![]() 轴正方向作匀速运动.同时点
轴正方向作匀速运动.同时点![]() 从点
从点![]() 出发以每秒1个单位长度沿
出发以每秒1个单位长度沿![]() 的路线作匀速运动,当
的路线作匀速运动,当![]() 点运动到
点运动到![]() 点时停止运动,矩形
点时停止运动,矩形![]() 也随之停止运动.设
也随之停止运动.设![]() 点运动时间为
点运动时间为![]() (秒).
(秒).
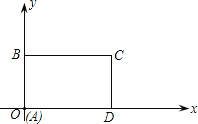
(1)当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(2)若![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的函数关系式(并写出相应的自变量
之间的函数关系式(并写出相应的自变量![]() 的取值范围).
的取值范围).
(3)画出题(2)所列的函数的大致图象.
【答案】(1)(12,3);(2)当0<t≤3时,s=t2;当3<t≤8时,s=3t;当8<t<11时,s=-t2+11t;(3)见解析
【解析】
(1)先判断出先P在边BC上,向右移动的单位数,再确定出矩形向右平移的单位数即可得出结论;
(2)分三种情况利用三角形的面积公式即可求解.
(3)在同一平面直角坐标系中分别画出三段函数在相应自变量范围内的图像即可.
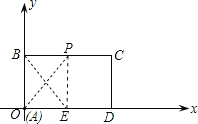
解:(1)当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3);
(2)分三种情况:
①0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=![]() ×2t×t=t2;
×2t×t=t2;
②3<t≤8时,点P在BC上运动,此时OA=2t
∴s=![]() ×2t×3=3t;
×2t×3=3t;
③8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)-(AB+BC+CP)=11-t
∴s=![]() ×2t×(11-t)=-t2+11t;
×2t×(11-t)=-t2+11t;
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=-t2+11t;
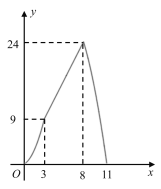
(3)根据(2)中三个函数可得如图:


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(题文)已知直线![]() 与抛物线
与抛物线![]() 相交于抛物线的顶点
相交于抛物线的顶点![]() 和另一点
和另一点![]() ,点
,点![]() 在第四象限.
在第四象限.
![]() 若点
若点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 过点
过点![]() 作
作![]() 轴的平行线与抛物线
轴的平行线与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个.
(1)为了使平均每月有10000元的销售利润,这种书包的售价应定为多少元?
(2)10000元的利润是否为最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价为多少元?
(3)请分析并回答售价在什么范围内商家就可以获得利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
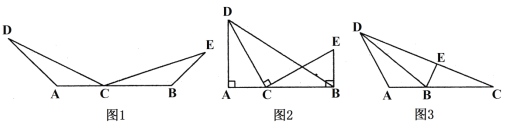
【题目】⑴如图1,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE,DC=CE.求证:AC=BE.
⑵如图2,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE=90°.
①求证:![]() ;②连接BD,若∠ADC=∠ABD,AC=3,BC=
;②连接BD,若∠ADC=∠ABD,AC=3,BC=![]() ,求tan∠CDB的值;
,求tan∠CDB的值;
⑶如图3,在△ABD中,点C在AB边上,且∠ADC=∠ABD,点E在BD边上,连接CE,∠BCE+∠BAD=180°,AC=3,BC=![]() ,CE=
,CE=![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为![]() 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为
的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为![]() ,种草所需费用
,种草所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为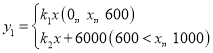 ,其大致图象如图所示.栽花所需费用
,其大致图象如图所示.栽花所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为![]() .
.
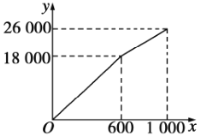
(1)求出![]() ,
,![]() 的值;
的值;
(2)若种花面积不小于![]() 时的绿化总费用为
时的绿化总费用为![]() (元),写出
(元),写出![]() 与
与![]() 的函数关系式,并求出绿化总费用
的函数关系式,并求出绿化总费用![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
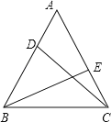
A.180°B.170°C.160°D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
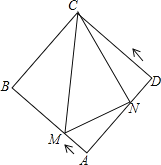
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
A. 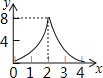 B.
B. 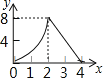
C. 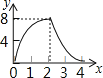 D.
D. 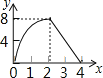
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城市化建设的发展,交通拥堵成为上班高峰时难以避免的现象.为了解龙泉驿某条道路交通拥堵情况,龙泉某中学同学经实地统计分析研究表明:当![]() 时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
时,车流速度v(千米/小时)是车流密度x(辆/千米)的一次函数.当该道路的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为95辆/千米时,车流速度为50千米/小时.
(1)当![]() 时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
时,求车流速度v(千米/小时)与车流密度x(辆/千米)的函数关系式;
(2)为使该道路上车流速度大于40千米/小时且小于60千米/小时,应控制该道路上的车流密度在什么范围内?
(3)车流量(辆/小时)是单位时间内通过该道路上某观测点的车辆数,即:车流量=车流速度×车流密度.当![]() 时,求该道路上车流量y的最大值.此时车流速度为多少?
时,求该道路上车流量y的最大值.此时车流速度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com