
分析 (1)先根据二次根式的除法和乘法法则运算,然后合并即可;
(2)先进行乘方运算,然后把除法运算化为乘法运算,再进行约分即可.
解答 解:①原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
②原式=-$\frac{{a}^{4}{b}^{3}}{{c}^{6}}$•$\frac{{c}^{2}}{{a}^{2}b}$•$\frac{{a}^{4}}{{b}^{4}{c}^{4}}$
=-$\frac{{a}^{6}}{{b}^{2}{c}^{8}}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了分式的乘除法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
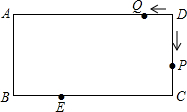 如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.
如图,在矩形ABCD中,AB=5cm,BC=10cm.动点P从点D出发,沿折线D-C-B-A-D以2cm/s的速度运动,动点Q从点D出发.沿D-A-B-C-D以1cm/s的速度运动.若动点P、Q同时出发,相遇是停止运动.设运动时间为ts.点E为BC边上一点,且BE=3cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
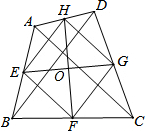 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.
如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
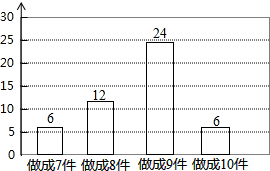 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )| A. | 12件 | B. | 8.625件 | C. | 8.5件 | D. | 9件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
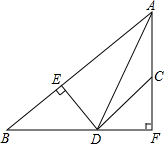 如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.
如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
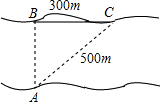 如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 300m,结果他在水中实际游了500m,求该河流的宽度为400m.
如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B 300m,结果他在水中实际游了500m,求该河流的宽度为400m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com