
����Ŀ����ũ��ʵ�д������е����ֲ��Ϊ�˸��õ��ո�ׯ�ڣ�ũ��а����Ŵ����������8̨�ո�������оñ���ʹ�������Ʒ�Ƶ��ո��������ÿ̨�ո���ļ۸�ÿ����ո�������±�![]() ������������˵������һ̨�ñ����ո���ȹ���һ̨�����ո����8��Ԫ������2̨�ñ����ո���ȹ���3̨�����ո����4��Ԫ��
������������˵������һ̨�ñ����ո���ȹ���һ̨�����ո����8��Ԫ������2̨�ñ����ո���ȹ���3̨�����ո����4��Ԫ��
�ñ����ո�� | �����ո�� | |
�۸� | x | y |
�ո���� | 24 | 18 |
![]() �������ո���ļ۸�
�������ո���ļ۸�
![]() ����Ŵ��幺���ո�����ʽ���125��Ԫ����ô���ļ��ֹ�����
����Ŵ��幺���ո�����ʽ���125��Ԫ����ô���ļ��ֹ�����
![]() ��
��![]() �������£���ÿ��Ҫ���ո����������150Ķ��Ϊ�˽�Լ�ʽ���ô��û��һ����ѹ����أ�
�������£���ÿ��Ҫ���ո����������150Ķ��Ϊ�˽�Լ�ʽ���ô��û��һ����ѹ����أ�
���𰸡�![]() �ñ����ո���ļ۸�Ϊÿ̨20��Ԫ�������ո���ļ۸�Ϊÿ̨12��Ԫ��
�ñ����ո���ļ۸�Ϊÿ̨20��Ԫ�������ո���ļ۸�Ϊÿ̨12��Ԫ��
![]() ������4�ֹ�����
������4�ֹ�����![]() �ñ����ո��3̨�������ո��5̨��
�ñ����ո��3̨�������ո��5̨��![]() �ñ����ո��2̨�������ո��6̨��
�ñ����ո��2̨�������ո��6̨��![]() �ñ����ո��1̨�������ո��7̨��
�ñ����ո��1̨�������ո��7̨��![]() �ñ����ո��0̨�������ո��8̨��
�ñ����ո��0̨�������ո��8̨��![]() ��ѹ���Ϊ�ñ����ո��1̨�������ո��7̨��
��ѹ���Ϊ�ñ����ո��1̨�������ո��7̨��
��������
![]() ������������ո���ļ۸�ֱ�Ϊx��Ԫ��y��Ԫ���������еĵ�����ϵ�г���Ԫһ�η������ɣ�
������������ո���ļ۸�ֱ�Ϊx��Ԫ��y��Ԫ���������еĵ�����ϵ�г���Ԫһ�η������ɣ�
![]() �蹺��ñ����ո��m̨
�蹺��ñ����ո��m̨![]() ���������ո�����ʽ���125��Ԫ���г�����m�IJ���ʽ��ͨ���ⲻ��ʽ�������m��ֵ��
���������ո�����ʽ���125��Ԫ���г�����m�IJ���ʽ��ͨ���ⲻ��ʽ�������m��ֵ��
![]() ����ÿ��Ҫ���ո����������150Ķ�г�����m�IJ���ʽ����ɣ�
����ÿ��Ҫ���ո����������150Ķ�г�����m�IJ���ʽ����ɣ�
![]() �������ո���ļ۸�ֱ�Ϊx��Ԫ��y��Ԫ��
�������ո���ļ۸�ֱ�Ϊx��Ԫ��y��Ԫ��
�������![]() ��
��
���![]() ��
��
�ʾñ����ո���ļ۸�Ϊÿ̨20��Ԫ�������ո���ļ۸�Ϊÿ̨12��Ԫ��
![]() �蹺��ñ����ո��m̨���������
�蹺��ñ����ո��m̨���������
![]() ���
���![]() ��
��
��������4�ֹ�����![]() �ñ����ո��3̨�������ո��5̨��
�ñ����ո��3̨�������ո��5̨��
![]() �ñ����ո��2̨�������ո��6̨��
�ñ����ո��2̨�������ո��6̨��
![]() �ñ����ո��1̨�������ո��7̨��
�ñ����ո��1̨�������ո��7̨��
![]() �ñ����ո��0̨�������ո��8̨��
�ñ����ո��0̨�������ո��8̨��
![]() ������ɵ�
������ɵ�![]() �����
�����![]() ��
��
��![]() �ù���ñ����ո��Խ��ԽʡǮ��������ѹ���Ϊ�ñ����ո��1̨�������ո��7̨��
�ù���ñ����ո��Խ��ԽʡǮ��������ѹ���Ϊ�ñ����ո��1̨�������ո��7̨��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=4��������ABCD�Ƶ�C��˳ʱ�뷽����ת���ǣ��õ�����A'B'C'D'��B'C��AD���ڵ�E��AD���ӳ�����A'D'���ڵ�F��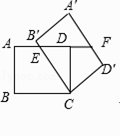
��1����ͼ�٣�����=60��ʱ������DD'����DD'��A'F�ij���
��2����ͼ�ڣ�������A'B'CD'�Ķ���A'����CD���ӳ�����ʱ����EF�ij���
��3����ͼ�ۣ���AE=EFʱ������AC��CF����ACCF��ֵ��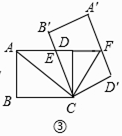
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�δ�ѧ��һ�꼶����ѵ����������У�ijС��ijɼ����
���� | 6 | 7 | 8 | 9 |
���� | 1 | 5 | 3 | 1 |
��1����С��������ݵ�������������
��2����С���ƽ���ɼ�Ϊ���٣���Ҫд��������̣�
��3����8������8��������Ϊ�������֣���1200���������ж����˿�����Ϊ�������֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OAƽ����EOC��

��1������EOC=70��������BOD�Ķ�����
��2������EOC����EOD=2��3������BOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���ֱ�ߺ�Բ������BAD��ƽ����AG��BC�ڵ�E����BF=6��AB=5����AE�ij�Ϊ�� �� 
A.4
B.6
C.8
D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=5��AC=6��BD=8�� 
��1����֤���ı���ABCD�����Σ�
��2������A��AH��BC�ڵ�H����AH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϊ�˽�ȫ�а��꼶ѧ������ѧ֪ʶ�������������һ����ѧ����У���ȫ��24000�����꼶�����������ȡ����ѧ������ѧ�ɼ����е��飬�������������Ƴ�����ͼ����
������ | Ƶ�� | Ƶ�� |
| 20 | 0.10 |
60�� | 28 | 0.14 |
70�� | 54 | 0.27 |
80�� |
| 0.20 |
90�� | 24 | 0.12 |
100�� | 18 |
|
110�� | 16 | 0.08 |

���������ͼ���ṩ����Ϣ������������⣺
��1������![]() ��
��![]() ����ʾ�����ֱ�Ϊ��
����ʾ�����ֱ�Ϊ��![]() = ��
= ��![]() = ��
= ��
��2������ͼ�У���ȫƵ���ֲ�ֱ��ͼ��
��3������ѳɼ���90�����ϣ���90�֣���Ϊ���㣬��ô����24000�����꼶������ѧ�ɼ�Ϊ�����ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��9+����7��+10+����3��+����9��
��2��12+����14��+6+����7��
��3���� ![]()
��4����4.2+5.7+����8.7��+4.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У�E��F�ֱ��DZ�AD��BC�ϵĵ㣬��AE=CF��ֱ��EF�ֱ�BA���ӳ��ߡ�DC���ӳ����ڵ�G��H����BD�ڵ�O��
��1����֤����ABE�ա�CDF��
��2������DG����DG=BG�����ı���BEDF��ʲô�����ı��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com