
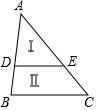
 如图:若平行于BC的直线DE把△ABC分成两部分,SⅠ:SⅡ=4:5,则$\frac{AD}{DB}$=2.
如图:若平行于BC的直线DE把△ABC分成两部分,SⅠ:SⅡ=4:5,则$\frac{AD}{DB}$=2. 分析 证明△ADE∽△ABC,得$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=$\frac{B{C}^{2}}{D{E}^{2}}$,再应用比例的性质及相似三角形的性质即可求解.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{BC}{DE}=\frac{AB}{AD}$
∴$\frac{{S}_{△ABC}}{{S}_{△ADE}}$=$\frac{B{C}^{2}}{D{E}^{2}}$,
∴$\frac{{S}_{△ABC}-{S}_{△ADE}}{{S}_{△ADE}}$=$\frac{B{C}^{2}-D{E}^{2}}{D{E}^{2}}$,
即:$\frac{B{C}^{2}-D{E}^{2}}{D{E}^{2}}$=$\frac{5}{4}$,
解得:$\frac{BC}{DE}$=$\frac{3}{2}$,即:$\frac{AB}{AD}$=$\frac{3}{2}$
∴$\frac{AB-AD}{AD}$=$\frac{3-2}{2}$=$\frac{1}{2}$
∴$\frac{DB}{AD}=\frac{1}{2}$
∴$\frac{AD}{DB}$=2
故答案为:2
点评 本题考查了相似三角形的判定与性质,解题的关键是熟练的应用比例的性质.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
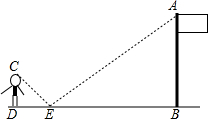 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
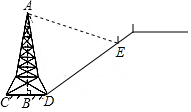 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为28.8m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
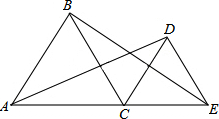 如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.
如图,已知C为线段AE上的一个动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,连接AD,BE,AC=5,AD=7,则BE=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
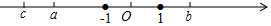
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
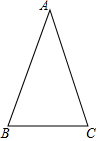 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com