
【题目】![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,点
,点![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 延长交
延长交![]() 于
于![]() ,
,![]() .小华得出
.小华得出![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() .
.
其中正确的是( )

A. ①② B. ①③ C. ②③ D. ①②③
【答案】D
【解析】
首先连接OE,CE,由OE=OD,PE=PF,易得∠OED+∠PEF=∠ODE+∠PFE,又由OD⊥BC,可得OE⊥PE,继而证得PE为⊙O的切线;
又由BC是直径,可得CE⊥AB,由切线长定理可得GC=GE,根据等角的余角相等,可得∠A=∠AEG,根据等腰三角形的判定,可得答案;
易证得OG是△ABC的中位线,则可得OG∥BE.
连接OE,CE.
∵OE=OD,PE=PF,∴∠OED=∠ODE,∠PEF=∠PFE.
∵OD⊥BC,∴∠ODE+∠OFD=90°.
∵∠OFD=∠PFE,∴∠OED+∠PEF=90°,即OE⊥PE.
∵点E在⊙O上,∴GE为⊙O的切线;
点C在⊙O上,OC⊥GC,∴GC为⊙O的切线,∴GC=GE.
故①正确;
∵BC是直径,∴∠BEC=90°,∴∠AEC=90°.
∵∠ACB=90°,∴AC是⊙O的切线,∴EG=CG,∴∠GCE=∠GEC.
∵∠GCE+∠A=90°,∠GEC+∠AEG=90°,∴∠A=∠AEG,∴AG=EG;故②正确;
∵OC=OB,AG=CG,∴OG是△ABC的中位线,∴OG∥AB;故③正确.
故选D.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:

A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=﹣x+3与x轴、y轴交于点A,点B,点O关于直线AB的对称点为点O′,且点O′恰好在反比例函数y=![]() 的图象上.
的图象上.
(1)求点A与B的坐标;
(2)求k的值;
(3)若y轴正半轴有点P,过点P作x轴的平行线,且与反比例函数y=![]() 的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=
的图象交于点Q,设A、P、Q、O′四个点所围成的四边形的面积为S.若S=![]() S△OAB时,求点P的坐标.
S△OAB时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AC的垂直平分线MN交AB于D,交AC于E.

(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,0),

(1)在图中作出线段AB以二四象限的角平分线为对称轴的对称线段CD,并直接写出四边形ABDC的面积为 ;
(2)若点C为格点(横纵坐标均为整数),且AB⊥OC,且AB=OC,作出线段OC;并写出C点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察与发现:小明将三角形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
边上,折痕为![]() ,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图②).小明认为
(如图②).小明认为![]() 是等腰三角形,你同意吗?请说明理由.
是等腰三角形,你同意吗?请说明理由.
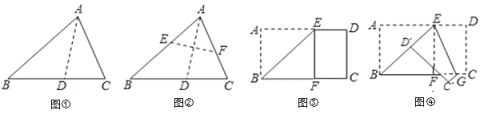
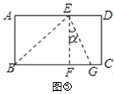
(2)实践与运用:将矩形纸片![]() 沿过点
沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() (如图③);再沿过点
(如图③);再沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() (如图④);再展平纸片(如图⑤).求图⑤中
(如图④);再展平纸片(如图⑤).求图⑤中![]() 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com