
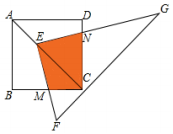
 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2.
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF,EG分别交BC,DC于点M,N,若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为$\frac{4}{9}$a2. 分析 过E作EP⊥BC于点P,EQ⊥CD于点Q,△EPM≌△EQN,利用四边形EMCN的面积等于正方形PCQE的面积求解.
解答 解:过E作EP⊥BC于点P,EQ⊥CD于点Q,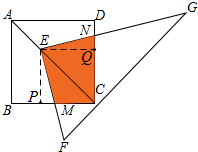
∵四边形ABCD是正方形,
∴∠BCD=90°,
又∵∠EPM=∠EQN=90°,
∴∠PEQ=90°,
∴∠PEM+∠MEQ=90°,
∵三角形FEG是直角三角形,
∴∠NEF=∠NEQ+∠MEQ=90°,
∴∠PEM=∠NEQ,
∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,
∴EP=EQ,四边形PCQE是正方形,
在△EPM和△EQN中,
$\left\{\begin{array}{l}{∠PEM=∠NEQ}\\{EP=EQ}\\{∠EPM=∠EQN}\end{array}\right.$,
∴△EPM≌△EQN(ASA)
∴S△EQN=S△EPM,
∴四边形EMCN的面积等于正方形PCQE的面积,
∵正方形ABCD的边长为a,
∴AC=$\sqrt{2}$a,
∵EC=2AE,
∴EC=$\frac{2\sqrt{2}}{3}$a,
∴EP=PC=$\frac{2}{3}$a,
∴正方形PCQE的面积=$\frac{2}{3}$a×$\frac{2}{3}$a=$\frac{4}{9}$a2,
∴四边形EMCN的面积=$\frac{4}{9}$a2,
故答案为:$\frac{4}{9}$a2.
点评 本题主要考查了正方形的性质及全等三角形的判定及性质,解题的关键是作出辅助线,证出△EPM≌△EQN.


科目:初中数学 来源: 题型:填空题
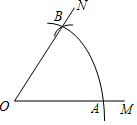 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
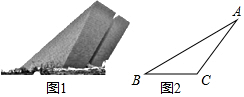 位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:$\sqrt{3}$,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
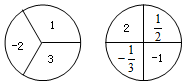 如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).
如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成 4 个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com