
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②3a+c>0;
③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
④当y>3时,x的取值范围是0≤x<2;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A.1个B.2个C.3个D.4个
【答案】C
【解析】
利用抛物线与x轴的交点个数可对①进行判断;由对称轴方程得到b=﹣2a,然后根据x=﹣1时函数值为0可得到3a+c=0,则可对②进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
解:∵抛物线与x轴有2个交点,
∴b2﹣4ac>0,所以①正确;
∵x=![]() =1,即b=﹣2a,
=1,即b=﹣2a,
而x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
所以②错误;
∵抛物线的对称轴为直线x=1,
而点(﹣1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=﹣1,x2=3,
所以③正确;
根据对称性,由图象知,
当0<x<2时,y>3,所以④错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
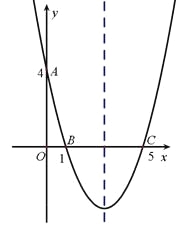
(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营业员![]() 人,某一月的销售量统计如下表所示:
人,某一月的销售量统计如下表所示:
公司![]() 名营业员某一月的销售量统计表
名营业员某一月的销售量统计表
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)求这![]() 名营业员该月销售量数据的平均数;
名营业员该月销售量数据的平均数;
(2)这![]() 名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)
名营业员该月销售量数据的中位数是 件,众数是 件,为了提高大多数营业员的积极性,实行“每天定额售量,超出有奖”的措施.如果你是管理者,你选择.确定“定额”的统计量为 (填“中位数”或“众数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某湖边健身步道全长1500米,甲、乙两人同时从同一起点匀速向终点步行.甲先到达终点后立刻返回,在整个步行过程中,甲、乙两人间的距离y(米)与出发的时间x(分)之间的关系如图中OA﹣AB折线所示.
(1)用文字语言描述点A的实际意义;
(2)求甲、乙两人的速度及两人相遇时x的值.
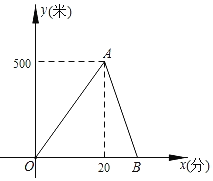
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连接AF,BF,EF,过点F作GF⊥AF交AD于点G,设![]() .
.
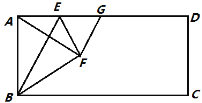
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=AC=![]() ,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
,∠B=30°,点O为边BC上一点以O为圆心的圆经过点A,B.
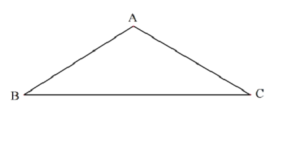
(1)求作圆O(尺规作图,保留作留痕迹,不写作法);
(2)求证:AC是OO的切线;
(3)若点P为圆O上一点,且弧PA=弧PB,连接PC,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列函数图象上任取不同两点P1(x1,y1)、P2(x2,y2),一定能使![]() <0成立的是( )
<0成立的是( )
A.y=3x﹣1(x<0)B.y=﹣x2+2x﹣1(x>0)
C.y=﹣![]() (x>0)D.y=x2﹣4x+1(x<0)
(x>0)D.y=x2﹣4x+1(x<0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数
,1)在反比例函数![]() 的图象上.
的图象上.

(1)求反比例函数![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP=![]() S△AOB,求点P的坐标;
S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com