
【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答: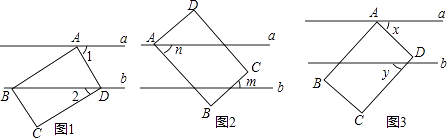
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1=;
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请写出m与n的数量关系并说明理由;
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.
【答案】
(1)60°
(2)解:如图2,过C作EF∥a,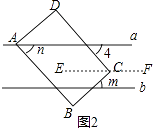
∵四边形ABCD是矩形,
∴AB∥CD,
∴n=∠4,
∵a∥b,EF∥a,
∴EF∥a∥b,
∴∠4=∠DCE ,∠ECB=m;
∴∠4+m=∠BCD=90°,
∴m+n=90°;
(3)解:如图3,过D作c∥b,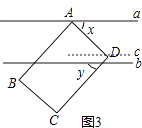
∵x2﹣2xy+y2=100,
∴(x﹣y)2=100,
∵x>y,
∴x﹣y=﹣10(舍去),
∴x﹣y=10,①
∵a∥b,c∥b,
∴a∥b∥c,
∵∠ADC=90°,
∴x+y=90,②
①+②得:x=50°.
【解析】(1)∵四边形ABCD是长方形,
∴∠ADC=90°,
∵∠2=30°,
∴∠ADB=60°,
∵a∥b,
∴∠1=∠ADB=60°,
故答案为:60°;
(1)根据矩形的四个角都是直角得出∠ADC=90°,根据角的和差得出∠ADB=60°,根据二直线平行内错角相等得出∠1=∠ADB=60°;
(2)过C作EF∥a,根据矩形的对边互相平行得出AB∥CD,根据二直线平行同位角相等得出n=∠4,根据平行于同一直线的两条直线互相平行得出EF∥a∥b,根据二直线平行,内错角相等得出∠4=∠DCE ,∠ECB=m;根据等式的性质得出结论;
(3)将方程x2﹣2xy+y2=100,利用直接开平方法得出x﹣y=10,①,根据平行于同一直线的两条直线互相平行得出a∥b∥c,根据二直线平行,内错角相等,及等式的性质得出结论。


科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
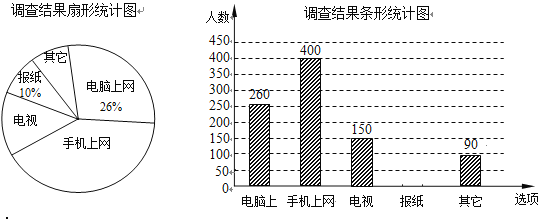
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于 ![]() EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 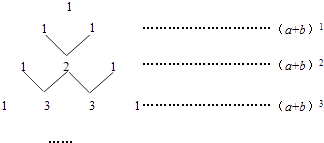
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com