
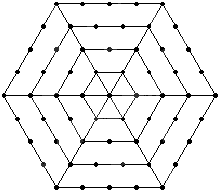
 如图是一个形如正六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,…,依此类推.
如图是一个形如正六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,…,依此类推.| 层数 | 1 | 2 | 3 | 4 | … |
| 该层对应的点数 | 1 | 6 | 12 | 18 | … |
| 所有层的总点数 | 1 | 7 7 |
19 19 |
37 37 |
… |
| n(n-1) |
| 2 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
 21、正方体是特殊的长方体,又称“立方体”、“正六面体”.
21、正方体是特殊的长方体,又称“立方体”、“正六面体”.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
课题:探究能拼成正多边形的三角形的面积计算公式.
1.如图1,三角形的三边长分别为a、b、c,∠A=60°,现将六个这样的三角形(设面积为![]() )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得![]() = .
= .
2.如图2, 三角形的三边长分别为a、b、c,∠A=120°,试用这样的三角形拼成一个正三角形(设面积为![]() ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出![]() 的计算公式;
的计算公式;
3.推广:
对于三角形的三边长分别为a、b、c,当∠A取什么值时,能拼成一个任意正![]() 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积![]() 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西省中等学校招生统一考试数学卷(二) 题型:解答题
课题:探究能拼成正多边形的三角形的面积计算公式.
【小题1】如图1,三角形的三边长分别为a、b、c,∠A=60°,现将六个这样的三角形(设面积为 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 = .
= .
【小题2】如图2, 三角形的三边长分别为a、b、c,∠A=120°,试用这样的三角形拼成一个正三角形(设面积为 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 的计算公式;
的计算公式;
【小题3】推广:
对于三角形的三边长分别为a、b、c,当∠A取什么值时,能拼成一个任意正 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年江西省等学校招生统一考试数学卷(二) 题型:解答题
课题:探究能拼成正多边形的三角形的面积计算公式.
1.如图1,三角形的三边长分别为a、b、c,∠A=60°,现将六个这样的三角形(设面积为 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 =
.
=
.
2.如图2, 三角形的三边长分别为a、b、c,∠A=120°,试用这样的三角形拼成一个正三角形(设面积为 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 的计算公式;
的计算公式;
3.推广:
对于三角形的三边长分别为a、b、c,当∠A取什么值时,能拼成一个任意正 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com