
分析 (1)由题意可知有三处可以藏身,所以小明在B处找到小红的概率为其中的三分之一;
(2)根据题意画树状图,然后根据树状图求得所有等可能的结果与小明在同一地点找到小红和小兵的情况,然后根据概率公式求解即可.
解答 解:
(1)∵小红、小兵可以在A、B、C三个地点中任意一处藏身,
∴小明在B处找到小红的概率=$\frac{1}{3}$;
(2)画树形图得: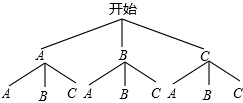
由树形图可知小明在同一地点找到小红和小兵的概率=$\frac{3}{9}$=$\frac{1}{3}$.
点评 此题考查了树状图法与列表法求概率.树状图法与列表法可以不重不漏的表示出所有等可能的情况.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
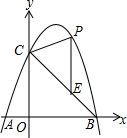 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
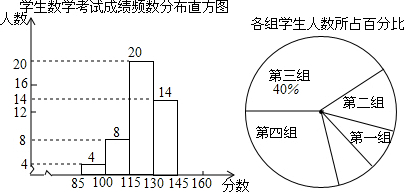
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.
如图,在矩形ABCD中,AB=2,BC=4,M是AD的中点,动点E在线段AB上,连结EM并延长交射线CD于点F,过点M作EF的垂线交BC于点G,连结EG、FG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com