
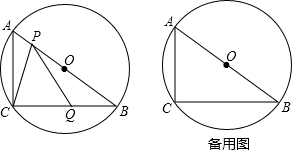
分析 (1)首先证明∠ACB=90°,然后利用勾股定理即可解决问题.
(2)如图2中,作PH⊥BC于H.由PH∥AC,推出$\frac{PH}{AC}$=$\frac{PB}{AB}$,推出$\frac{PH}{6}$=$\frac{10-x}{10}$,推出PH=$\frac{3}{5}$(10-x),根据y=$\frac{1}{2}$•CQ•PH计算即可.
(3)因为△CPQ与△ABC相似,∠CPQ=∠ACB=90°,又因为∠CQP>∠B,所以只有∠PCB=∠B,推出PC=PB,由∠B+∠A=90°,∠ACP+∠PCB=90°,推出∠A=∠ACP,推出PA=PC=PB=5,由△COQ∽△BCA,推出$\frac{CO}{BC}$=$\frac{CQ}{AB}$,推出$\frac{5}{8}$=$\frac{8-5k}{10}$,即可解决问题.
解答 解:(1)∵AB是直径,
∴∠ACB=90°,∵AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴⊙O的半径为5.
(2)如图2中,作PH⊥BC于H.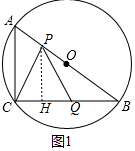
∵PH∥AC,
∴$\frac{PH}{AC}$=$\frac{PB}{AB}$,
∴$\frac{PH}{6}$=$\frac{10-x}{10}$,
∴PH=$\frac{3}{5}$(10-x),
∴y=$\frac{1}{2}$•CQ•PH=$\frac{1}{2}$•(8-2x)•$\frac{3}{5}$(10-x)=$\frac{3}{5}$x2-$\frac{42}{5}$x+24(0<x<4).
(3)如图2中,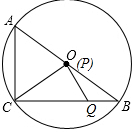
∵△CPQ与△ABC相似,∠CPQ=∠ACB=90°,
又∵∠CQP>∠B,
∴只有∠PCB=∠B,
∴PC=PB,
∵∠B+∠A=90°,∠ACP+∠PCB=90°,
∴∠A=∠ACP,
∴PA=PC=PB=5,
∴△COQ∽△BCA,
∴$\frac{CO}{BC}$=$\frac{CQ}{AB}$,
∴$\frac{5}{8}$=$\frac{8-5k}{10}$,
∴k=$\frac{7}{20}$.
点评 本题考查圆综合题、平行线分线段成比例定理、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,正确应用相似三角形的性质解决问题,学会用构建方程的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
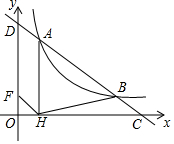 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
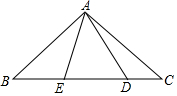 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$).(用含a、b的式子表示AB)
如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB.设BE=a,DC=b,那么AB=$\frac{\sqrt{2}}{2}$(a+b+$\sqrt{{a}^{2}+{b}^{2}}$).(用含a、b的式子表示AB)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 价格类型 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
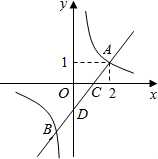 如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
如图,一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com