
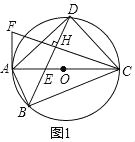
【题目】已知四边形ABCD为⊙O的内接四边形,直径AC与对角线BD相交于点E,作CH⊥BD于H,CH与过A点的直线相交于点F,∠FAD=∠ABD.
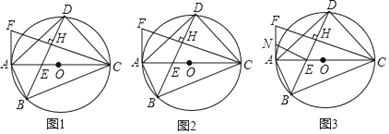
(1)求证:AF为⊙O的切线;
(2)若BD平分∠ABC,求证:DA=DC;
(3)在(2)的条件下,N为AF的中点,连接EN,若∠AED+∠AEN=135°,⊙O的半径为2![]() ,求EN的长.
,求EN的长.
【答案】(1)见解析;(2)见解析;(3)NE=![]()
【解析】
(1)欲证明AF为⊙O的切线,只需推知CA⊥AF;
(2)如图2,连接OD.理由圆周角定理和等量代换推知:∠DOA=∠DOC,则DA=DC.
(3)如图3,连接OD交CF于M,作EP⊥AD于P.构造全等三角形:△ODE≌△OCM,则OE=OM,设OM=m,所以AE=2![]() ﹣m,AP=PE=2﹣
﹣m,AP=PE=2﹣![]() m,DP=2+
m,DP=2+![]() m;由△EAN∽△DPE的对应边成比例推知:
m;由△EAN∽△DPE的对应边成比例推知:![]() =
=![]() ,所以
,所以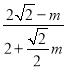 =
=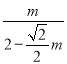 ,求出m=
,求出m=![]() ,得到AN=
,得到AN=![]() ,AE=
,AE=![]() ,结合勾股定理得NE=
,结合勾股定理得NE=![]() .
.
(1)证明:如图1,∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°.
∵![]() ,
,
∴∠ABD=∠DCA,
∵∠FAD=∠ABD,
∴∠FAD=∠DCA,
∴∠FAD+∠DCA=90°,
∴CA⊥AF,
∴AF为⊙O的切线.
(2)证明:如图2,连接OD,
∵![]() ,
,
∴∠ABD=![]() ∠AOD,
∠AOD,
∵![]() ,
,
∴∠DBC=![]() ∠DOC,
∠DOC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠DOA=∠DOC,
∴DA=DC.
(3)如图3,连接OD交CF于M,作EP⊥AD于P,
∵AC为⊙O的直径,
∴∠ADC=90°.
∵DA=DC,
∴DO⊥AC,
∴∠FAC=∠DOC=90°,
∴AF∥OM,
∵AO=OC,
∴OM=![]() AF.
AF.
∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°.
∴∠ODE=∠OCM.
∵∠DOE=∠COM,OD=OC,
∴∴△ODE≌△OCM,
∴OE=OM,
设OM=m,
∴AE=2![]() ﹣m,AP=PE=2﹣
﹣m,AP=PE=2﹣![]() m,DP=2+
m,DP=2+![]() m,
m,
∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,
∴∠AEN=∠ADE,
∵∠EAN=∠DPE,
∴△EAN∽△DPE,
∴![]() =
=![]() ,
,
∴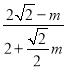 =
=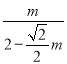 ,
,
∴m=![]() ,
,
∴AN=![]() ,AE=
,AE=![]() ,
,
∴勾股定理得NE=![]() .
.




科目:初中数学 来源: 题型:
【题目】超速行驶被称为“马路第一杀手”,为了让驾驶员自觉遵守交通规则,市公路检测中在一事故多发地段安装了一个测速仪器,如图所示,已知检测点A设在距离公路BC20米处,∠B=45°,∠C=30°,现测得一辆汽车从B处行驶到C处所用时间为2.7秒.
(1)求B,C之间的距离(结果保留根号);
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() 1.7,
1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)某校九年级数学课外兴趣探究小组在学习完《第二十八章锐角三角函数》后,利用所学知识进行深度探究,得到以下正确的等量关系式:
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
,
(理解应用)请你利用以上信息求下列各式的值:(1)![]() ;(2)
;(2)![]()
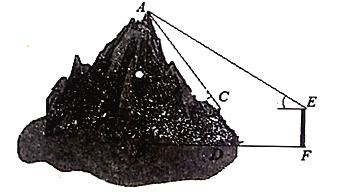
(拓展应用)(3)为了求出海岛上的山峰![]() 的高度,在
的高度,在![]() 处和
处和![]() 处树立标杆
处树立标杆![]() 和
和![]() ,标杆的高都是3丈,
,标杆的高都是3丈,![]() 两处相隔1000步(1步等于6尺),并且
两处相隔1000步(1步等于6尺),并且![]() 和
和![]() 在同一平面内,在标杆
在同一平面内,在标杆![]() 的顶端
的顶端![]() 处测得山峰顶端
处测得山峰顶端![]() 的仰角75°,在标杆
的仰角75°,在标杆![]() 的顶端
的顶端![]() 处测得山峰顶端
处测得山峰顶端![]() 的仰角30°,山峰的高度即
的仰角30°,山峰的高度即![]() 的长是多少步?(结果保留整数)(参考数据:
的长是多少步?(结果保留整数)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由两个可以自由转动的转盘、每个转盘被分成如图所示的几个扇形、游戏者同时转动两个转盘,如果一个转盘转出了红色,另一转盘转出了蓝色,游戏者就配成了紫色下列说法正确的是( )
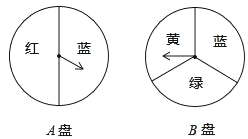
A. 两个转盘转出蓝色的概率一样大
B. 如果A转盘转出了蓝色,那么B转盘转出蓝色的可能性变小了
C. 先转动A 转盘再转动B 转盘和同时转动两个转盘,游戏者配成紫色的概率不同
D. 游戏者配成紫色的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为x=1的抛物线经过A(﹣1,0),B(2,﹣3)两点.
(1)求抛物线的解析式;
(2)P是抛物线上的动点,连接PO交直线AB于点Q,当Q是OP中点时,求点P的坐标;
(3)C在直线AB上,D在抛物线上,E在坐标平面内,以B,C,D,E为顶点的四边形为正方形,直接写出点E的坐标.
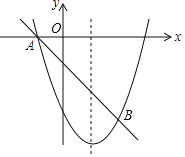
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如下方法,将△ABC的三边缩小到原来的![]() ,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是( )
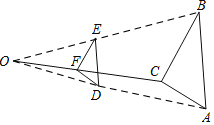
A.点O为位似中心且位似比为1:2
B.△ABC与△DEF是位似图形
C.△ABC与△DEF是相似图形
D.△ABC与△DEF的面积之比为4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,己知点![]() ,点
,点![]() 在
在![]() 轴上,并且
轴上,并且![]() ,动点
,动点![]() 在过
在过![]() 三点的拋物线上.
三点的拋物线上.
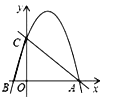
(1)求抛物线的解析式.
(2)作垂直![]() 轴的直线,在第一象限交直线
轴的直线,在第一象限交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,求当线段
,求当线段![]() 的长有最大值时
的长有最大值时![]() 的坐标.并求出
的坐标.并求出![]() 最大值是多少.
最大值是多少.
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得△
,使得△![]() 是等腰三角形?若存在,请直接写出点
是等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com