
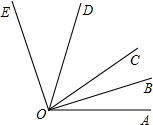
 如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是________;若以OB为钟表上的时针,OD为分针,且OB在2小时~3小时之间,请写出此刻的时间________.
如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是________;若以OB为钟表上的时针,OD为分针,且OB在2小时~3小时之间,请写出此刻的时间________. 分.
分. ∠AOE,通过计算即可推出的结果;
∠AOE,通过计算即可推出的结果; ∠EOC+
∠EOC+ ∠AOC=
∠AOC= (∠EOC+∠AOC)=
(∠EOC+∠AOC)= ∠AOE=55°;
∠AOE=55°; x+60-6x=55
x+60-6x=55 ,
, 分.
分. 分.
分.

科目:初中数学 来源: 题型:
 如图已知FB∥ED,AB∥DC,∠B=50°,求∠D的度数.
如图已知FB∥ED,AB∥DC,∠B=50°,求∠D的度数.查看答案和解析>>
科目:初中数学 来源: 题型:
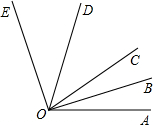 如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是
如图已知∠AOE=110°,射线OD、OB分别是∠EOC、∠COA的角平分线.则∠BOD的度数是| 10 |
| 11 |
| 10 |
| 11 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,已知:在梯形ABCD中,CD∥AB,AD、BC的延长线相交于点E,AC、BD相交于点O,连接EO并延长交AB于点M,交CD于点N.则S△AOE:S△BOE等于( )
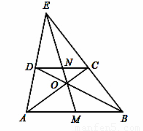
A.1∶1???????? B.4∶3????????? C.3∶4????????????? D.3∶2
查看答案和解析>>
科目:初中数学 来源:浙江省期末题 题型:填空题
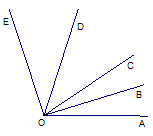
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com