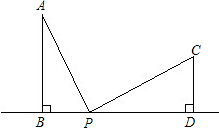
解:(1)由AB=6cm,CD=4cm,BD=14cm,
设BP=xcm,则PD=(14-x)cm,
若△ABP∽△PDC,
∴

=
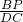
,即
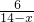
=

,
变形得:14x-x
2=24,即x
2-14x+24=0,
因式分解得:(x-2)(x-12)=0,
解得:x
1=2,x
2=12,
∴BP=2cm或12cm时,△ABP∽△PDC;
若△ABP∽△CDP,

=
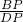
,即

=

,解得:x=8.4,
∴BP=8.4cm,
综上,BP=2cm或12cm或8.4cm时,△ABP∽△PDC;
(2)若∠APC=90°,则∠APB+∠CPD=90°,
又AB⊥BD,CD⊥BD,∴∠B=∠D=90°,
∴∠A+∠APB=90°,
∴∠A=∠CPD,
∴△ABP∽△PDC,
由(1)得此时BP=2cm或12cm,
则当BP=2cm或12cm时,∠APC=90°.
分析:(1)设出BP=xcm,由BD-BP=PD表示出PD的长,若△ABP∽△PDC,根据相似三角形的对银边成比例可得比例式,把各边的长代入即可列出关于x的方程,求出方程的解即可得到x的值,即为PB的长;
(2)若∠APC=90°,根据平角的定义可得剩下的两个角之和为90°,又根据AB⊥BD,CD⊥BD,得到一对直角相等,在直角三角形ABP中可得一对锐角之和为90°,等量代换可得∠A=∠CPD,根据两对对应角相等的两三角形相似可得△ABP∽△PDC,由(1)推出的三角形相似时BP的长可得解.
点评:此题考查了相似三角形的判定与性质,相似三角形的性质有相似三角形的对应边成比例,对应角相等;相似三角形的判定方法有:1、两对对应角相等的两三角形相似;2、两对对应边成比例且夹角相等的两三角形相似;3、三边对应成比例的两三角形相似,本题属于条件开放型探究题,其解法:类似于分析法,假设结论成立,逐步探索其成立的条件.

 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动, 解:(1)由AB=6cm,CD=4cm,BD=14cm,
解:(1)由AB=6cm,CD=4cm,BD=14cm, =
=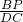 ,即
,即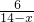 =
= ,
, =
=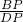 ,即
,即 =
= ,解得:x=8.4,
,解得:x=8.4,

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案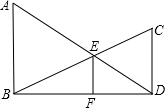 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明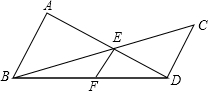
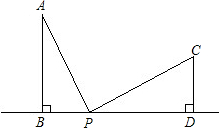 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,