
【题目】解答题
(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4,求正六边形的边长. 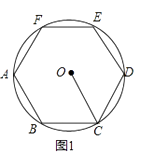
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC. 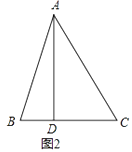
【答案】
(1)解:连接OD,如图所示:
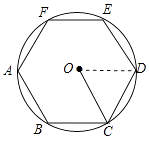
∵六边形ABCDEF是圆O的内接正六边形,
∴∠O= ![]() =60°,
=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
即正六边形的边长为4
(2)证明:∵AD是△ABC的中线,
∴BD=CD= ![]() BC=5,
BC=5,
∵AB=13,AD=12,
∴BD2+AD2=52+122=169=132=AB2,
∴△ABD是直角三角形,AD⊥BC,
又∵BD=CD,
∴AB=AC.
【解析】(1)连接OD,求出∠O=60°,证出△OCD是等边三角形,得出CD=OC=4即可;(2)由勾股定理的逆定理证出AD⊥BC,再由线段垂直平分线的性质即可得出AB=AC.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对正多边形和圆的理解,了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知a>b,请用“>”或“<”填空:
(1)a-1________b-1;(2)![]() a________
a________![]() b;(3)a+c________b+c;(4)-3a________-3b;(5)-
b;(3)a+c________b+c;(4)-3a________-3b;(5)-![]() a-c________-
a-c________-![]() b-c.
b-c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.
x2+bx+c交x轴于点A(2,0)、B(一8,0),交y轴于点C,过点A、B、C三点的⊙M与y轴的另一个交点为D.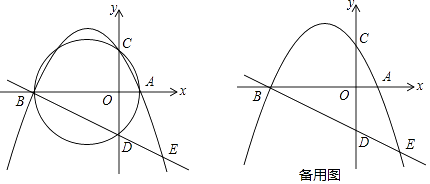
(1)求此抛物线的表达式及圆心M的坐标;
(2)设P为弧BC上任意一点(不与点B,C重合),连接AP交y轴于点N,请问:APAN是否为定值,若是,请求出这个值;若不是,请说明理由;
(3)延长线段BD交抛物线于点E,设点F是线段BE上的任意一点(不含端点),连接AF.动点Q从点A出发,沿线段AF以每秒1个单位的速度运动到点F,再沿线段FB以每秒 ![]() 个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
个单位的速度运动到点B后停止,问当点F的坐标是多少时,点Q在整个运动过裎中所用时间最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1 , y1),(x2 , y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2 , 请你类比此方法,推断方程x3+x﹣1=0的实数根x0所在范围为( )
A.﹣ ![]() <x0<0
<x0<0
B.0<x0< ![]()
C.![]() <x0<1
<x0<1
D.1<x0< ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点 A1、A2、A3、…在射线 ON 上,点 B1、B2、B3、…在射线 OM 上;△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形.若 OA1=1,则△A2015B2015A2016 的边长为 ( )
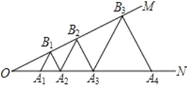
A. 4028 B. 4030 C. 22014 D. 22015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):﹣6,﹣3,x,2,﹣1,3,若这组数据的中位数是﹣1,在下列结论中:①方差是8;②极差是9;③众数是﹣1;④平均数是﹣1,其中正确的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形,寻找对顶角(不含平角).
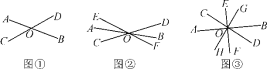
(1)如图①,图中共有______对对顶角;
(2)如图②,图中共有______对对顶角;
(3)如图③,图中共有______对对顶角;
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成__________对对顶角;
(5)若20条直线相交于一点,则可形成对顶角多少对?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com