
 ,梯形的高
,梯形的高 ,且
,且 .
. 时,求作以CF、DF的长为根的一元二次方程.
时,求作以CF、DF的长为根的一元二次方程.
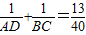 化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数.
化简,可得出关于AD,BC的和与BC的比例关系,让两个式子相除即可得出AD的值,也就能求出BC,AB的长了.有了AB的长,那么可在直角三角形ABE中,根据AB,AE的值用正弦函数求出∠B的度数. (AD+BC)•AE,S△ABC=
(AD+BC)•AE,S△ABC= BC•AE
BC•AE =
=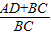 =
=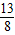 …①
…①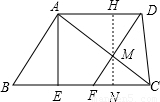
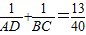
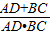 =
=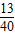 …②
…②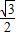
 AD•MH=
AD•MH= ×5•MH=
×5•MH=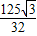


科目:初中数学 来源:2001年全国中考数学试题汇编《二次函数》(02)(解析版) 题型:解答题
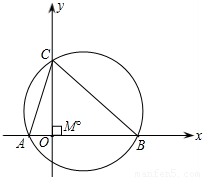
查看答案和解析>>
科目:初中数学 来源:2001年全国中考数学试题汇编《一次函数》(02)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2001年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2001年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com