
分析 当△ADB是以AD为腰的等腰三角形,可以分两种情况进行讨论:①AD=AB,②AD=BD;
①当AD=AB时,又分两种情况:
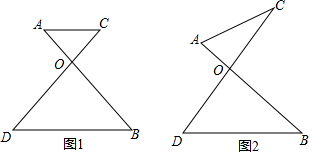
当点D在AC边上方时,如图1所示.由△ACD为等边三角形,得∠CAD=60°,根据角的关系可得结论;
当点D在AC边下方时,如图2所示.同理可得结论;
②当AD=BD时又分两种情况:
当点D在BC的上方,如图3所示.作辅助线,证明∠EDA=∠ADC,根据角平分线的性质得:AF=AE=$\frac{1}{2}$AB=$\frac{1}{2}$AC,利用直角三角形30°角的判定得:Rt△AFC中,∠ACF=30°,从而得出结论;
当D在BC的下方时,如图4,同理构建矩形AEFC,由CF=$\frac{1}{2}$AB=$\frac{1}{2}$AC=$\frac{1}{2}$CD,得Rt△CFD中,∠CDF=30°,可得结论.
解答 解:①当AD=AB时,
∵AB=AC,CD=AC,AD=AB,
∴AC=AD=CD,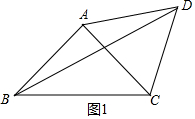
∴△ACD为等边三角形.
当点D在AC边上方时,如图1所示.
∵△ABC是等腰直角三角形,AB=AC,△ACD为等边三角形,
∴∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC+∠CAD=150°.
∵AB=AD,
∴∠ABD=∠ADB=$\frac{1}{2}$(180°-∠BAD)=15°,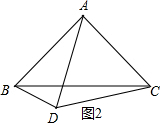
∴∠CDB=∠ADC-∠ADB=60°-15°=45°;
当点D在AC边下方时,如图2所示.
∵∠BAC=90°,∠CAD=60°,
∴∠BAD=∠BAC-∠CAD=30°.
∵AB=AD,
∴∠ABD=∠ADB=$\frac{1}{2}$(180°-∠BAD)=75°,
∴∠CDB=∠ADB+∠ADC=75°+60°=135°.
②当AD=BD时,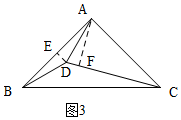
当点D在BC的上方,如图3所示.
过D作DE⊥AB于E,过A作AF⊥CD于F,
∴∠BED=90°,
∵∠BAC=90°,
∴∠BED=∠BAC,
∴ED∥AC,
∴∠EDA=∠DAC,
∵AD=CD,
∴∠ADC=∠DAC,
∴∠EDA=∠ADC,
∴AF=AE=$\frac{1}{2}$AB=$\frac{1}{2}$AC,
Rt△AFC中,∠ACF=30°,
∴∠ADC=$\frac{180°-30°}{2}$=75°,
∴∠ADB=2∠ADE=2∠ADC=150°,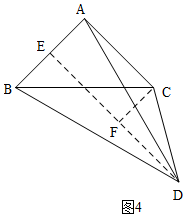
∴∠CDB=360°-150°-75°=135°;
当D在BC的下方时,如图4,
过D作DE⊥AC于E,过C作CF⊥ED于F,
∴∠AEF=∠BAC=∠EFC=90°,
∴四边形AEFC是矩形,
∴CF=AE,
∵AD=BD,DE⊥AB,
∴AE=$\frac{1}{2}$AB,∠ADE=∠BDE,
∴CF=$\frac{1}{2}$AB=$\frac{1}{2}$AC=$\frac{1}{2}$CD,
Rt△CFD中,∠CDF=30°,
∵AC∥ED,
∴∠CAD=∠ADE,
∵AC=CD,
∴∠CAD=∠ADC,
∴∠CDA=∠ADE=$\frac{1}{2}$∠CDF=15°,
∴∠ADB=30°,
∴∠CDB=45°.
综上所述,则∠CDB的度数为45°或135°;
故答案为:45°或135°.
点评 本题考查了等腰三角形的性质和判定、等腰直角三角形的性质和判定、角平分线的性质、中垂线的性质以及直角三角形30°的判定,本题多解,要注意不要丢解,采用了分类讨论的思想,并利用数形结合,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )
如图,正方形ABCD的边长为4,点E是正方形外一动点,∠AED=45°,P为AB的中点,当E运动时,线段PE的最大值为( )| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -2 | C. | 0 | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
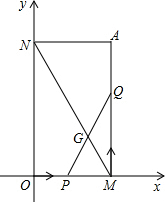 如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.
如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
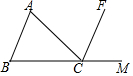 如图,点C在射线BM上,CF是∠ACM的平分线,且CF∥AB,∠ACB=50°,则∠B的度数为( )
如图,点C在射线BM上,CF是∠ACM的平分线,且CF∥AB,∠ACB=50°,则∠B的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
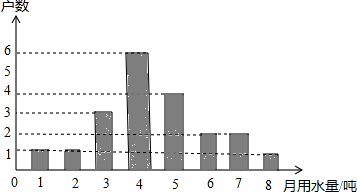 张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图.
张小花是社区宣传干部,为宣传节约用水,他随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图的统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com