
【题目】计算:
(1)3y2-2y+4y2;
(2)![]() +4-3st-4;
+4-3st-4;
(3)2(2ab+3a)-3(2a-ab);
(4)a2-[-4ab+(ab-a2)]-2ab.
(5).(-1)3-![]() ÷3×[3-(-3)2];
÷3×[3-(-3)2];
(6)![]() ×
×![]() ÷(-9+19);
÷(-9+19);
(7)-24×![]() ;
;
(8)(-81)÷![]() +
+![]() ÷(-16);
÷(-16);
【答案】解:(1) 7y2-2y,(2)![]() ,(3)7ab,(4)2a2+ab,(5)0,(6)
,(3)7ab,(4)2a2+ab,(5)0,(6)![]() ,(7)2,(8)-
,(7)2,(8)-![]()
【解析】
根据整式的运算法则,有理数的运算法则,去括号法则进行解题即可.
解:(1)3y2-2y+4y2
=(3y2+4y2) -2y
=7y2-2y
(2)![]() +4-3st-4
+4-3st-4
=(![]() -3st)+(4-4)
-3st)+(4-4)
=![]()
(3)2(2ab+3a)-3(2a-ab)
=4ab+6a-6a+3ab
=7ab
(4)a2-[-4ab+(ab-a2)]-2ab
=a2-(-4ab+ ab-a2) -2ab
=a2+4ab-ab+a2-2ab
=2a2+ab
(5).(-1)3-![]() ÷3×[3-(-3)2]
÷3×[3-(-3)2]
=-1-![]() ×
×![]() ×(-6)
×(-6)
=-1+1
=0
(6)![]() ×
×![]() ÷(-9+19)
÷(-9+19)
=![]() ×
×![]() ×
×![]()
=![]()
=![]()
(7)-24×![]()
=24×![]() -24×
-24×![]() +24×
+24×![]()
=12-18+8
=2
(8)(-81)÷![]() +
+![]() ÷(-16)
÷(-16)
=(-81)×![]() +
+![]() ×(-
×(-![]() )
)
=-36-![]()
=-![]()


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
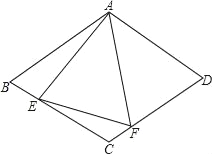
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
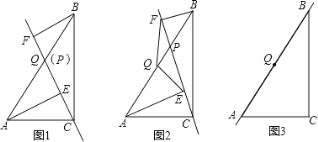
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系式 ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
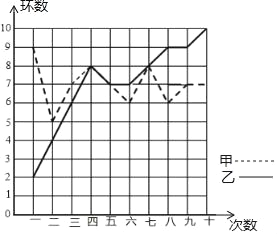
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
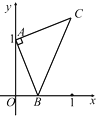
【题目】如图,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 是
是![]() 轴正半轴上的一动点,以
轴正半轴上的一动点,以![]() 为边作等腰直角
为边作等腰直角![]() ,使
,使![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,能表示
,能表示![]() 与
与![]() 的函数关系的图象大致是
的函数关系的图象大致是
A. 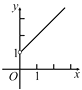 B.
B. 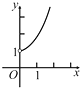 C.
C. 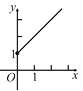 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的定价为每件20元,商场为了促销,决定如果购买5件以上,则超过5件的部分打7折.
(1)求购买这种商品的货款y (元)与购买数量x (件)之间的函数关系;
(2)当x=3,x=6时,货款分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
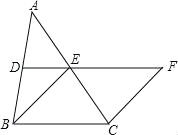
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=2,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数的图象经过A(0,﹣6)、B(4,﹣6)、C(6,0)三点.
(1)求这个二次函数的解析式;
(2)分别联结AC、BC,求tan∠ACB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com