
分析 (1)分两种情况讨论:①当k=1时,方程是一元一次方程,有实数根;②当k≠1时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)由韦达定理得x1+x2=-$\frac{2k}{k-1}$,x1x2=$\frac{2}{k-1}$,代入到$\frac{{x}_{2}}{{x}_{1}}$$+\frac{{x}_{1}}{{x}_{2}}$+x1+x2=2中,可求得k的值.
解答 解:(1)当k=1时,原方程可化为2x+2=0,解得:x=-1,此时该方程有实根;
当k≠1时,方程是一元二次方程,
∵△=(2k)2-4(k-1)×2
=4k2-8k+8
=4(k-1)2+4>0,
∴无论k为何实数,方程总有实数根,
综上所述,无论k为何实数,方程总有实数根.
(2)由根与系数关系可知,x1+x2=-$\frac{2k}{k-1}$,x1x2=$\frac{2}{k-1}$,
若S=2,则$\frac{{x}_{2}}{{x}_{1}}$$+\frac{{x}_{1}}{{x}_{2}}$+x1+x2=2,即$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$+x1+x2=2,
将x1+x2、x1x2代入整理得:k2-3k+2=0,
解得:k=1(舍)或k=2,
∴S的值能为2,此时k=2.
点评 本题主要考查一元二次方程的定义、根的判别式、根与系数的关系,熟练掌握方程的根与判别式间的联系,及根与系数关系是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
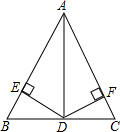 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )
如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )| A. | 10cm | B. | 15cm | C. | 10$\sqrt{3}$cm | D. | 20$\sqrt{2}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com