
分析 根据根与系数的关系得到x1+x2=$\frac{5}{2}$,x1x2=$\frac{1}{2}$,再计算$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$的值得到$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$=$\frac{21}{2}$,设$\frac{{x}_{1}}{{x}_{2}}$=t,所以t+$\frac{1}{t}$=$\frac{21}{2}$,然后解关于t的方程即可.
解答 解:根据题意得x1+x2=$\frac{5}{2}$,x1x2=$\frac{1}{2}$,
所以$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\frac{25}{4}-2×\frac{1}{2}}{\frac{1}{2}}$=$\frac{21}{2}$,
设$\frac{{x}_{1}}{{x}_{2}}$=t,
则t+$\frac{1}{t}$=$\frac{21}{2}$,
整理得2t2-21t+2=0,解得t=$\frac{21±5\sqrt{17}}{4}$,
所以$\frac{{x}_{1}}{{x}_{2}}$的值为$\frac{21±5\sqrt{17}}{4}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:填空题
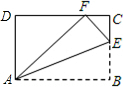 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.
如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
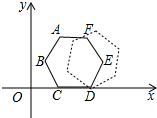 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com