
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.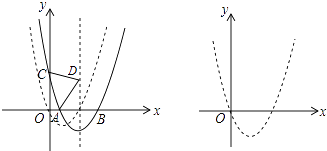
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
【答案】
(1)解:∵抛物线C1经过原点,与X轴的另一个交点为(2,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线C1的解析式为y=x2﹣2x,
∴抛物线C1的顶点坐标(1,﹣1).
(2)解:如图1,
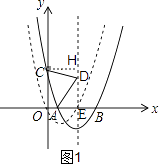
∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,
∴C2的解析式为y=(x﹣m﹣1)2﹣1,
∴A(m,0),B(m+2,0),C(0,m2+2m),
过点C作CH⊥对称轴DE,垂足为H,
∵△ACD为等腰直角三角形,
∴AD=CD,∠ADC=90°,
∴∠CDH+∠ADE=90°
∴∠HCD=∠ADE,
∵∠DEA=90°,
∴△CHD≌△DEA,
∴AE=HD=1,CH=DE=m+1,
∴EH=HD+DE=1+m+1=m+2,
由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),
∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)解:如图2,连接BC,BP,
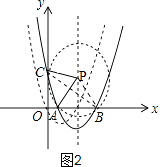
由抛物线对称性可知AP=BP,
∵△PAC为等边三角形,
∴AP=BP=CP,∠APC=60°,
∴C,A,B三点在以点P为圆心,PA为半径的圆上,
∴∠CBO= ![]() ∠CPA=30°,
∠CPA=30°,
∴BC=2OC,
∴由勾股定理得OB= ![]() =
= ![]() OC,
OC,
∴ ![]() (m2+2m)=m+2,
(m2+2m)=m+2,
解得m1= ![]() ,m2=﹣2(舍去),∴m=
,m2=﹣2(舍去),∴m= ![]() .
.
【解析】(1)把(0,0)及(2,,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标.
(2)先求出C2的解析式,确定A、B、C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△ACD为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值即可得出抛物线C2的解析式.
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=![]() OC,列出方程求出m的值即可.
OC,列出方程求出m的值即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述正确的是( )
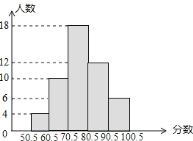
A.抽样的学生共60人
B.60.5~70.5这一分数段的频数为12
C.估计这次测试的及格率(60分为及格)在92%左右
D.估计优秀率(80分以上为优秀)在32%左右
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )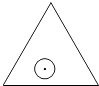
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)能使S△ABC=S△QBC的格点Q(A点除外)共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程 ![]() 有两个不相等的实数根,
有两个不相等的实数根,
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠A=90°,AB=AC,∠ABC 的角平分线交 AC 于 D,BD=4 ![]() ,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )
,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )

A.![]() B.2
B.2 ![]() C.3
C.3 ![]() D.2
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以OA为边的△OAB面积为2,其中点B的横、纵坐标均不超过4,且都不小于0,在下列叙述中,正确的是:_____.(请写出所有正确的选项)
①若点B的横坐标是4,则满足条件的点B有且只有1个;
②若点B是整点(即横、纵坐标都是整数),则满足条件的点B有4个;
③在坐标系内,对于任意满足题意的点B,一定存在一点C,使得△CAB、△COA、△COB面积相等;
④在坐标系内,存在一个定点D,使得对于任意满足条件的点B,△DBA、△DBO面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为![]() ,若
,若![]() ,则
,则![]() 的值是_______.
的值是_______.
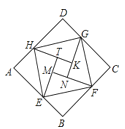
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com