
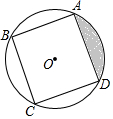
 如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )
如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( )| A. | π+1 | B. | π+2 | C. | π-1 | D. | π-2 |
分析 根据对称性可知阴影部分的面积等于圆的面积减去正方形的$\frac{1}{4}$,求出圆内接正方形的边长,即可求解.
解答 解:连接AO,DO,
∵ABCD是正方形,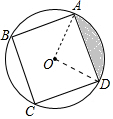
∴∠AOD=90°,
AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=2$\sqrt{2}$,
圆内接正方形的边长为2$\sqrt{2}$,所以阴影部分的面积=$\frac{1}{4}$[4π-(2$\sqrt{2}$)2]=(π-2)cm2.
故选D.
点评 本题考查正多边形与圆、正方形的性质、圆的面积公式、扇形的面积公式等知识,解题的关键是利用对称性可知阴影部分的面积等于圆的面积减去正方形的$\frac{1}{4}$,也可以用扇形的面积减去三角形的面积计算,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | -8 | C. | $\frac{1}{16}$ | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=2 | B. | a=-3,b=2 | C. | a=3,b=-1 | D. | a=-1,b=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m$>\frac{8}{9}$ | C. | m=$\frac{9}{8}$ | D. | m=$\frac{8}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 2.0 | C. | 2.02 | D. | 2.03 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+2)2+1 | B. | y=(x+2)2-1 | C. | y=(x-2)2+1 | D. | y=(x-2)2-1 |
查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:填空题
如图,在⊙O中, 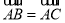 ,∠AOB=40°,则∠ADC的度数是 _______。
,∠AOB=40°,则∠ADC的度数是 _______。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com