
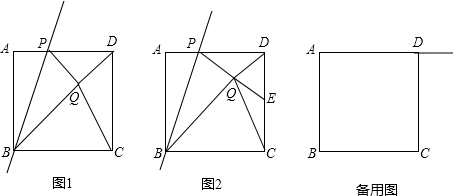
分析 (1)BQ+DQ为点B到D两段折线的和.由两点间线段最短可知,连接DB,若Q点落在BD上,此时和最短,且为$\sqrt{2}$.考虑动点运动,这种情形是存在的,由AP=x,则PD=1-x,PQ=x.又∠PDQ=45°,所以PD=$\sqrt{2}$PQ,即1-x=$\sqrt{2}$x.求解可得x=$\sqrt{2}$-1.
(2)①由已知条件对称分析,AB=BQ=BC,则∠BCQ=∠BQC,由∠BQE=∠BCE=90°,可得∠EQC=∠ECQ即可.
②通常都是考虑勾股定理,选择直角三角形PDE,发现PE,DE,PD都可用x来表示,进而易得方程,求解即可.
(3)若△CDQ为等腰三角形,则边CD比为改等腰三角形的一腰或者底边.又Q点为A点关于PB的对称点,则AB=QB,以点B为圆心,以AB的长为半径画弧,则Q点只能在弧AB上.若CD为腰,以点C为圆心,以CD的长为半径画弧,两弧交点即为使得△CDQ为等腰三角形(CD为腰)的Q点.若CD为底边,则作CD的垂直平分线,其与弧AC的交点即为使得△CDQ为等腰三角形(CD为底)的Q点.则如图所示共有三个Q点,那么也共有3个P点.作辅助线,利用直角三角形性质求之即可
解答 解:(1)连接DB,若Q点落在BD上,此时和最短,且为$\sqrt{2}$,
由AP=x,则PD=1-x,PQ=x.
∵∠PDQ=45°,
∴PD=$\sqrt{2}$PQ,即1-x=$\sqrt{2}$x.
∴x=$\sqrt{2}$-1,
故答案为:$\sqrt{2}$,$\sqrt{2}$-1
(2)①证明:在正方形ABCD中,
AB=BC,∠A=∠BCD=90°.
∵Q点为A点关于BP的对称点,
∴AB=QB,∠A=∠PQB=90°,
∴QB=BC,∠BQE=∠BCE,
∴∠BQC=∠BCQ,
∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ,
∴EQ=EC.
②解:∵AP=x,AD=1,
∴PD=1-x,PQ=x,CD=1.
在Rt△DQC中,
∵E为CD的中点,
∴DE=QE=CE=$\frac{1}{2}$,
∴PE=PQ+QE=x+$\frac{1}{2}$,
∴$(x+\frac{1}{2})^{2}=(1-x)^{2}+\frac{1}{4}$,
解得 x=$\frac{1}{3}$.
(3)答:△CDQ为等腰三角形时x的值为2-$\sqrt{3}$,$\frac{\sqrt{3}}{3}$,2+$\sqrt{3}$.
如图1,
以点B为圆心,以AB的长为半径画弧,以点C为圆心,以CD的长为半径画弧,两弧分别交于Q1,Q3.
此时△CDQ1,△CDQ3都为以CD为腰的等腰三角形.
作CD的垂直平分线交弧AC于点Q2,此时△CDQ2以CD为底的等腰三角形.
①如图2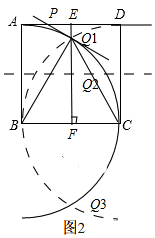 ,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.
,连接BQ1、CQ1,作PQ1⊥BQ1交AD于P,过点Q1,作EF⊥AD于E,交BC于F.
∵△BCQ1为等边三角形,正方形ABCD边长为1,
∴Q1F=$\frac{\sqrt{3}}{2}$Q1E=$\frac{2-\sqrt{3}}{2}$.
在四边形ABPQ1中,
∵∠ABQ1=30°,
∴∠APQ1=150°,
∴△PEQ1为含30°的直角三角形,
∴PE=$\sqrt{3}$Q1E=$\frac{2\sqrt{3}-3}{2}$.
∵AE=$\frac{1}{2}$,
∴x=AP=AE-PE=2-$\sqrt{3}$.
②如图3 ,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.
,连接BQ2,AQ2,过点Q2作PG⊥BQ2,交AD于P,连接BP,过点Q2作EF⊥CD于E,交AB于F.
∵EF垂直平分CD,
∴EF垂直平分AB,
∴AQ2=BQ2.
∵AB=BQ2,
∴△ABQ2为等边三角形.
在四边形ABQP中,
∵∠BAD=∠BQP=90°,∠ABQ2=60°,
∴∠APE=120°
∴∠EQ2G=∠DPG=180°-120°=60°,
∴Q2E=$\frac{2-\sqrt{3}}{2}$,
∴EG=$\frac{2\sqrt{3}-3}{2}$,
∴DG=DE+GE=$\sqrt{3}$-1,
∴PD=1-$\frac{\sqrt{3}}{3}$,
∴x=AP=1-PD=$\frac{\sqrt{3}}{3}$.
③如图4, 连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.
连接BQ1,CQ1,BQ3,CQ3,过点Q3作BQ3⊥PQ3,交AD的延长线于P,连接BP,过点Q1,作EF⊥AD于E,此时Q3在EF上,不妨记Q3与F重合.
∵△BCQ1为等边三角形,△BCQ3为等边三角形,BC=1,
∴Q1Q2=$\sqrt{3}$,Q1E=$\frac{2-\sqrt{3}}{2}$,
∴EF=$\frac{2+\sqrt{3}}{2}$.
在四边形ABQ3P中
∵∠ABF=∠ABC+∠CBQ3=150°,
∴∠EPF=30°,
∴EP=$\sqrt{3}$EF=$\frac{2\sqrt{3}+3}{2}$.
∵AE=$\frac{1}{2}$,
∴x=AP=AE+PE=$\sqrt{3}$+2.
综上所述,△CDQ为等腰三角形时x的值为2-$\sqrt{3}$,$\frac{\sqrt{3}}{3}$,2+$\sqrt{3}$.
点评 此题是四边形的综合题,主要考查了正方形的性质,等腰三角形的性质,勾股定理,直角三角形的性质,对称性,画出图形是解本题的关键,也是难点,是一道比较难点压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
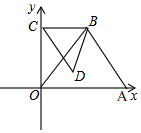 如图,直角坐标系中,O为原点,A(6,0),在等腰三角形ABO中,OB=BA=5,点B在第一象限,C(0,k)为y轴正半轴上一动点,作以∠CBD为顶角的等腰三角形CBD,且∠CBD=∠OBA,连结AD.
如图,直角坐标系中,O为原点,A(6,0),在等腰三角形ABO中,OB=BA=5,点B在第一象限,C(0,k)为y轴正半轴上一动点,作以∠CBD为顶角的等腰三角形CBD,且∠CBD=∠OBA,连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com