
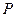 为圆心,1为半径作
为圆心,1为半径作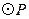 .
.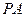 ,若
,若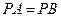 ,试判断
,试判断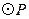 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;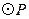 与直线AB相切?当
与直线AB相切?当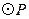 与直线AB相交时,写出PC的取值范围为 ;
与直线AB相交时,写出PC的取值范围为 ;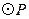 与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.
与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.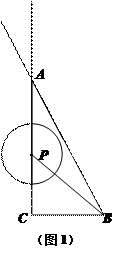
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:计算题
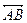 的中点,CD是⊙O的直径,过C点的直线
的中点,CD是⊙O的直径,过C点的直线 交AB所在直线于点E,交⊙O于点F。
交AB所在直线于点E,交⊙O于点F。 与
与 的数量关系,并写出结论;
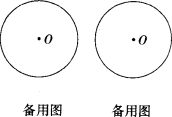
的数量关系,并写出结论; 绕C点旋转(与CD不重合),在旋转过程中,E点、F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明。
绕C点旋转(与CD不重合),在旋转过程中,E点、F点的位置也随之变化,请你在下面两个备用图中分别画出在不同位置时,使(1)的结论仍然成立的图形,标上相应字母,选其中一个图形给予证明。
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.DE="DO" | B.AB=AC |
| C.CD="DB" | D.AC∥OD |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
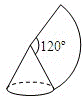
| A.3 | B.6 |
| C.9 | D.12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,并说明理由;
,并说明理由;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
2,BC=2,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.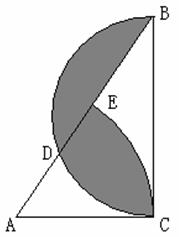
 ).
).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com