
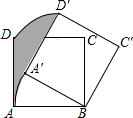
 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$. 分析 先根据正方形的性质求出BD,再根据旋转得到∠ABA′=∠DBD′=30°,判断出S阴影=S扇形DBD′-S扇形ABA′即可.
解答 解:如图,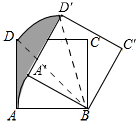
连接BD′,BD,
∵正方形ABCD边长为3,
∴BD=3$\sqrt{2}$,
∵正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,
∴∠ABA′=∠DBD′=30°,
∴S扇形DBD′=$\frac{30°×π×B{D}^{2}}{360°}$=$\frac{30°×π×(3\sqrt{2})^{2}}{360°}$=$\frac{3π}{2}$,
S扇形ABA′=$\frac{30°×π×A{B}^{2}}{360°}$=$\frac{30°×π×9}{360°}$=$\frac{3π}{4}$,
S阴影=S扇形DBD′+S△ABD-S△A′BD′-S扇形ABA′=S扇形DBD′-S扇形ABA′=$\frac{3π}{2}$-$\frac{3π}{4}$=$\frac{3}{4}π$.
点评 此题是旋转的性质,主要考查了旋转的性质,正方形的性质,扇形的面积的计算,分析出阴影部分的面积是两个扇形面积的差是解本题的关键也是难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
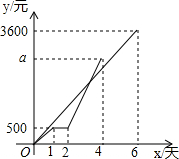 甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:
甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
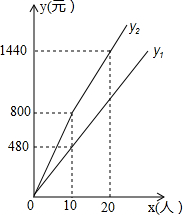 某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.
某景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用y1(元)及节假日门票费用y2(元)与游客x(人)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
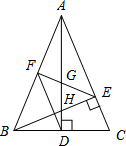 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确的有( )| A. | 1个 | B. | 2 个 | C. | 3 个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com