
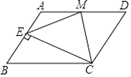
【题目】如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.
(1)求平行四边形ABCD的面积S;
(2)求证:∠EMC=2∠AEM.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由AM=2AE=4,利用平行四边形的性质可求出BC=AD=8,利用直角三角形的性质得出BE、CE的长,进而得出答案;
(2) 延长EM,CD交于点N,连接CM.通过证明△AEM≌△DNM,可得EM=MN,然后由直角三角形斜边的中线等于斜边的一半可证MN=MC,然后根据三角形外角的性质证明即可.
(1)解:∵M为AD的中点,AM=2AE=4,
∴AD=2AM=8.在ABCD的面积中,BC=CD=8,
又∵CE⊥AB,
∴∠BEC=90°,
∵∠BCE=30°,
∴BE=![]() BC=4,
BC=4,
∴AB=6,CE=4![]() ,
,
∴ABCD的面积为:AB×CE=6×4![]() =24
=24![]() ;
;
(2)证明:延长EM,CD交于点N,连接CM.
∵在ABCD中,AB∥CD,
∴∠AEM=∠N,
在△AEM和△DNM中
∵∠AEM=∠N,
AM=DM,
∠AME=∠DMN,
∴△AEM≌△DNM(ASA),
∴EM=MN,
又∵AB∥CD,CE⊥AB,
∴CE⊥CD,
∴CM是Rt△ECN斜边的中线,
∴MN=MC,
∴∠N=∠MCN,
∴∠EMC=2∠N=2∠AEM.


科目:初中数学 来源: 题型:
【题目】在同一平面内,两条直线相交时最多有1个交点,三条直线相交时最多有3个交点,四条直线相交时最多有6个交点,…,那么十条直线相交时最多有____个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)
如图①,AB∥CD,点M在直线AB、CD之间,则∠M=∠B+∠D,小明解决上述问题的过程如下:
如图②,过点M作MN∥AB
则∠B=_______(_______)
∵AB∥CD,(已知)
MN∥AB(辅助线的做法)
∴MN∥CD(______)
∴∠______=∠D(______)
∴∠B+∠D=∠BMD
请完成小明上面的过程.

(问题迁移)
如图③,AB∥CD,点M与直线CD分别在AB的两侧,猜想∠M、∠B、∠D之间有怎样的数量关系,并加以说明.
(推广应用)
(1)如图④,AB∥CD,点M在直线AB、CD之间,∠ABM的平分线与∠CDM的平分线交于点N,∠M=96°,则∠N=_____°;
(2)如图⑤,AB∥CD,点M与直线CD分别在AB的两侧,∠ABM的平分线与∠CDM的平分线交于点N,∠N=25°,则∠M=______°;
(3)如图⑥,AB∥CD,∠ABG的平分线与∠CDE的平分线交于点M,∠G=78°,∠F=64°,∠E=64°,则∠M=_______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() =8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
=8,则点A(1,a)关于y轴的对称点为点B,将点B向下平移2个单位后,再向左平移3个单位得到点C,则C点与原点及A点所围成的三角形的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作题
(1)画图并填空.
已知△ABC中,∠ACB = 90°,AC = 3个单位,BC = 4个单位.(1)画出把△ABC 沿射线BC方向平移2个单位后得到△DEF;直接写出△DCF的面积为 .

(2)小明有一张边长为13cm的正方形纸片(如图1),他想将其剪拼成一块一边为8cm,的长方形纸片.他想了一下,不一会儿就把原来的正方形纸片剪拼成了一张宽8cm,长21cm的长方形纸片(如图2),你认为小明剪拼得对吗?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com